题目内容
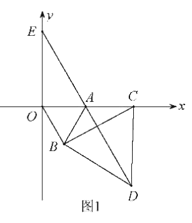
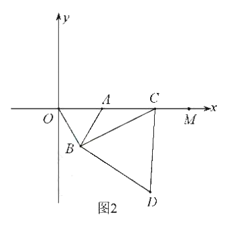
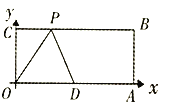
【题目】已知,如图,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 为矩形,
为矩形,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上运动,当
上运动,当![]() 是腰长为5的等腰三角形,则
是腰长为5的等腰三角形,则![]() 点的坐标为_________________________。
点的坐标为_________________________。
【答案】![]() ,
,![]() 或
或![]()
【解析】
分PD=OD(P在右边),PD=OD(P在左边),OP=OD(P在y轴右边),OP=OD(P在y轴左边)四种情况,根据题意画出图形,作PQ垂直于x轴,找出直角三角形,根据勾股定理求出OQ,然后根据图形写出P的坐标即可.
解:当OD=PD(P在右边)时,根据题意画出图形,如图所示: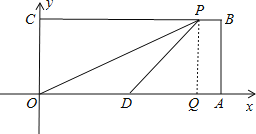
过P作PQ⊥x轴交x轴于Q,在直角三角形DPQ中,PQ=4,PD=OD=![]() OA=5,
OA=5,
根据勾股定理得:DQ=3,故OQ=OD+DQ=5+3=8,则P1(8,4);
当PD=OD(P在左边)时,根据题意画出图形,如图所示:
过P作PQ⊥x轴交x轴于Q,在直角三角形DPQ中,PQ=4,PD=OD=5,
根据勾股定理得:QD=3,故OQ=OD-QD=5-3=2,则P2(2,4);
当PO=OD(P在y轴右边)时,根据题意画出图形,如图所示: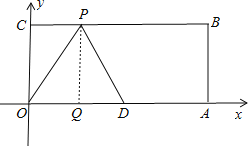
过P作PQ⊥x轴交x轴于Q,在直角三角形OPQ中,OP=OD=5,PQ=4,
根据勾股定理得:OQ=3,则P3(3,4),
当PO=OD(P在y轴左边)时,根据题意画出图形,如图所示: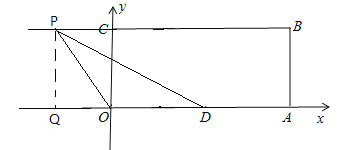
过P作PQ⊥x轴交x轴于Q,在直角三角形OPQ中,OP=OD=5,PQ=4,
根据勾股定理得:OQ=3,则P4(-3,4),
综上,满足题意的P坐标为(2,4),(3,4),(8,4)或![]() .
.
故答案为:(2,4),(3,4),(8,4)或![]() .
.

【题目】下面表格是某次篮球联赛部分球队不完整的积分表:
队名 | 比赛场数 | 胜场 | 负场 | 积分 |
前进 | 14 | 10 | 4 | 24 |
光明 | 14 | 9 | 5 | 23 |
远大 | 14 |
|
| 22 |
卫星 | 14 | 4 | 10 |
|
钢铁 | 14 | 0 | 14 | 14 |
请根据表格提供的信息:
(1)求出![]() 的值;
的值;
(2)请直接写出![]() ______,
______,![]() ______.
______.
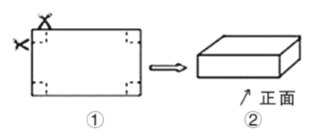
【题目】如图①是一张长为18![]() ,宽为12
,宽为12![]() 的长方形硬纸板,把它的四个角都剪去一个边长为
的长方形硬纸板,把它的四个角都剪去一个边长为![]() 的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积![]()
![]() ;(用含
;(用含![]() 的代数式表示即可,不需化简)
的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当![]() 取什么正整数时,长方体盒子的容积最大?
取什么正整数时,长方体盒子的容积最大?
| 1 | 2 | 3 | 4 | 5 |
| 160 | ________ | 216 | ________ | 80 |
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出![]() 的值;如果不是正方形,请说明理由.
的值;如果不是正方形,请说明理由.