题目内容
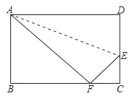
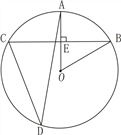
【题目】如图,直线AB,CD交于点O,OE平分![]() ,OF是
,OF是![]() 的角平分线.
的角平分线.
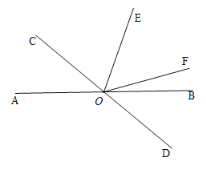
(1)说明: ![]() ;
;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)57.5;(3)40
【解析】
(1)根据角平分线的定义可得∠COB=2∠COE,然后根据对顶角相等可得∠AOD=∠COB,从而证出结论;
(2)根据对顶角相等和平角的定义即可求出∠BOD和∠COB,然后根据角平分线的性质即可求出∠EOB,从而求出∠EOD,再根据角平分线的定义即可求出∠EOF;
(3)设∠AOC=x°,根据对顶角相等可得∠BOD=∠AOC=x°,利用角的关系和角平分线的定义分别用x表示出∠DOF、∠EOF、∠EOB、∠COB,然后利用∠AOC+∠COB=180°列方程即可求出∠AOC.
解:(1)∵OE平分![]() ,
,
∴∠COB=2∠COE
∵∠AOD=∠COB
∴∠AOD=2∠COE
(2)∵![]() ,
,
∴∠BOD=∠AOC=50°,∠COB=180°-∠AOC=130°
∵OE平分![]() ,
,
∴∠EOB=![]() ∠COB=65°
∠COB=65°
∴∠EOD=∠EOB+∠BOD=115°
∵OF是![]() 的角平分线
的角平分线
∴∠EOF=![]() ∠EOD=
∠EOD=![]()
(3)设∠AOC=x°
∴∠BOD=∠AOC=x°
∴∠DOF=∠BOD+∠BOF=(x+15)°
∵OF是![]() 的角平分线
的角平分线
∴∠EOF=∠DOF= (x+15)°
∴∠EOB= ∠EOF+∠BOF=(x+30)°
∵OE平分![]() ,
,
∴∠COB=2∠EOB=(2x+60)°
∵∠AOC+∠COB=180°
∴x+(2x+60)=180
解得x=40
∴∠AOC=40°

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解我市市区初中生“绿色出行”方式的情况,某初中数学兴趣小组以问卷调查的形式,随机调查了本校部分学生上下学的主要出行方式,并将调查结果绘制了如图所示的两幅不完整的统计图,请根据图中提供的信息解答以下问题:
种类 |
|
|
|
|
|
出行方式 | 步行 | 公交车 | 自行车 | 私家车 | 出租车 |
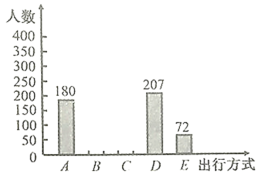
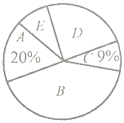
(1)参与本次问卷调查的学生共有_________人,其中选择![]() 类的人数所占的百分比为____________.
类的人数所占的百分比为____________.
(2)请通过计算补全条形统计图,并计算扇形统计图中![]() 类所对应扇形的圆心角的度数.
类所对应扇形的圆心角的度数.
(3)我市市区初中生每天约![]() 人出行,若将
人出行,若将![]() ,
,![]() ,
,![]() 这三类出行方式均视为“绿色出行”方式,请估计我市市区初中生选取“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市市区初中生选取“绿色出行”方式的人数.
【题目】某区举行“中华诵![]() 经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图

根据以上信息,整理分析数据如下:
平均数(分 | 中位数(分 | 众数(分 | |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
(1)写出表格中![]() ,
,![]() ,
,![]() 的值:
的值:![]() ,
,![]() ,
,![]() .
.
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较稳定.
【题目】下面表格是某次篮球联赛部分球队不完整的积分表:
队名 | 比赛场数 | 胜场 | 负场 | 积分 |
前进 | 14 | 10 | 4 | 24 |
光明 | 14 | 9 | 5 | 23 |
远大 | 14 |
|
| 22 |
卫星 | 14 | 4 | 10 |
|
钢铁 | 14 | 0 | 14 | 14 |
请根据表格提供的信息:
(1)求出![]() 的值;
的值;
(2)请直接写出![]() ______,
______,![]() ______.
______.