题目内容
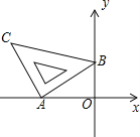
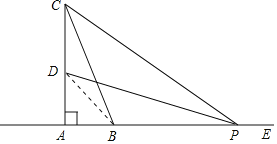
【题目】如图,在△ABC中,∠BAC=90°,AB=5cm,BC=13cm,点D在线段AC上,且CD=7cm,动点P从距B点15cm的E点出发,以每秒2cm的速度沿射线EA的方向运动,时间为t秒.
(1)求AD的长.
(2)用含有t的代数式表示AP的长.
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.
(4)直接写出t=______秒时,△PBC为等腰三角形.
【答案】(1)5cm;(2)PA=![]() ;(3)t的值为4或16;(4)1或14或12.5或
;(3)t的值为4或16;(4)1或14或12.5或![]() .
.
【解析】
(1)利用勾股定理求出AC的长即可解决问题;
(2)根据线段的和差关系可求出AE的长,根据距离=速度×时间可求出PE的长,根据绝对值的定义即可表示出AP的长;
(3)当AC=PA时,△ABC与△ADP全等,列方程即可求出t的值;
(4)分三种情形:BC=BP,BC=CP,PC=PB分别求解即可.
(1)在Rt△ABC中,∵∠BAC=90°,AB=5cm,BC=13cm,
∴AC=![]() =
=![]() =12(cm),
=12(cm),
∵CD=7cm,
∴AD=AC﹣CD=12﹣7=5(cm).
(2)∵AB=5,BE=15,
∴AE=BE+AB=20,
∵点P以每秒2cm的速度沿射线EA的方向运动,
∴PE=2t,
∴AP=![]() =
=![]() ,
,
(3)∵AD=BD=5cm,∠BAC=∠PAD=90°,
∴当AC=PA时,△ABC与△ADP全等,
∴![]() =12,
=12,
解得:t=4或t=16,
∴满足条件的t的值为4或16.
(4)当BC=BP时,![]() =13,
=13,
解得t=1或t=14,
当CP=CB时,PA=AB=5,
∴![]() =5,
=5,
t=12.5或t=7.5,
∵t=7.5时,点P与点B重合,不符合题意,
∴t=12.5.
当PC=PB时,122+(20-2t)2=(2t﹣15)2,
解得:t=![]() ,
,
故答案为:1或14或12.5或![]()

【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
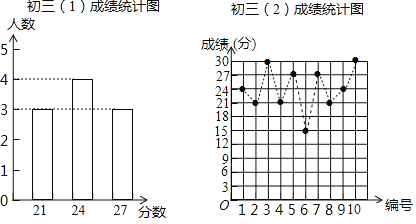
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 |
初三(1)班 | __________ | 24 | ________ |
初三(2)班 | 24 | _________ | 21 |
(2)若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)观察上图的数据分布情况,请通过计算说明哪个班的学生纠错的得分更稳定.