Question

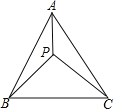
【题目】已知，P为等边三角形ABC内一点，PA＝3，PB＝4，PC＝5，则S△ABC＝_____．

Answer 1

【答案】

【解析】

将△BPC绕点B逆时针旋转60°得△BEA，根据旋转的性质得BE＝BP＝4，AE＝PC＝5，∠PBE＝60°，则△BPE为等边三角形，得到PE＝PB＝4，∠BPE＝60°，在△AEP中，AE＝5，延长BP，作AF⊥BP于点F，根据勾股定理的逆定理可得到△APE为直角三角形，且∠APE＝90°，即可得到∠APB的度数，在Rt△APF中利用三角函数求得AF和PF的长，则在Rt△ABF中利用勾股定理求得AB的长，进而求得三角形ABC的面积．

解：∵△ABC为等边三角形，

∴BA＝BC，

可将△BPC绕点B逆时针旋转60°得△BEA，

连EP，且延长BP，作AF⊥BP于点F．如图，

∴BE＝BP＝4，AE＝PC＝5，∠PBE＝60°，

∴△BPE为等边三角形，

∴PE＝PB＝4，∠BPE＝60°，

在△AEP中，AE＝5，AP＝3，PE＝4，

∴AE2＝PE2+PA2，

∴△APE为直角三角形，且∠APE＝90°，

∴∠APB＝90°+60°＝150°．

∴∠APF＝30°，

∴在直角△APF中，AF＝AP＝，PF＝AP＝．

∴在直角△ABF中，AB2＝BF2+AF2＝（4+）2+（）2＝25+12．

∴△ABC的面积＝AB2＝（25+12）＝；

故答案为：．