��Ŀ����
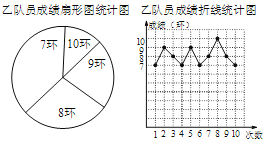
����Ŀ��ij��������Ӽס���������Ա��ѡȡһ����Ա�����öӲμӱ�������Ϊ�ס���������Ա������һ��ѡ������Ҫ����������Ա�����10��.�����������ݱ����ɼ���������ס���������Ա�ı����ɼ��Ƴ������µ�ͳ��ͼ(��)��
��Ա�ijɼ�ͳ�Ʊ�
�ɼ�(��λ����) | 7 | 8 | 9 | 10 |
����(�����) | 5 | 1 | 2 | 2 |
(1)��ͼ1�У�����8�����������ε�Բ�ĽǵĶ�����
(2)�����������õ��ķ����������������е�a��b��c��ֵ.
��Ա | ƽ���� | ��λ�� | ���� | ���� |
�� | 8 | 7.5 | 7 | c |
�� | a | b | 7 | 1 |
(3)���ݼס���������Ա�ijɼ���������������ѡ���Ҳμӱ���������д��һ�������ѡ���ҵ�����.
���𰸡�(1)108����(2)a=8��b=8��c=1.5��(3)�ҵķ���С˵���ҵijɼ��ȶ�.
��������
(1)��360�����Զ�Ӧ������ռ������
(2)����ƽ��������λ��������Ķ������ɵã�
(3)���Դ���λ���ͷ���ĽǶȽ�𣬴𰸲�Ψһ.
�⣺(1)��ͼ1�У���8�����������ε�Բ�ĽǵĶ���Ϊ360���![]() ��108����
��108����
(2)a��![]() ��8��
��8��
b��![]() ��8��
��8��
c��![]() ��[(7��8)2��5+(8��8)2+(9��8)2��2+(10��8)2��2]��1.5��
��[(7��8)2��5+(8��8)2+(9��8)2��2+(10��8)2��2]��1.5��
(3)�ҵķ���С˵���ҵijɼ��ȶ�(�𰸲�Ψһ).

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ