题目内容
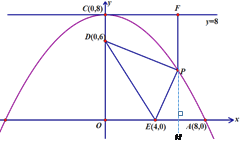
【题目】如图，抛物线的顶点坐标为C（0，8），并且经过A（8，0），点P是抛物线上点A，C间的一个动点（含端点），过点P作直线y=8的垂线，垂足为点F，点D，E的坐标分别为（0，6），（4，0），连接PD，PE，DE．
（1）求抛物线的解析式；
（2）猜想并探究：对于任意一点P，PD与PF的差是否为固定值？如果是，请求出此定值；如果不是，请说明理由；
（3）求：①当△PDE的周长最小时的点P坐标；②使△PDE的面积为整数的点P的个数．
【答案】（1）抛物线的解析式为y=﹣
x2+8；（2）PD与PF的差是定值，PD﹣PF=2；（3）①P（4，6），此时△PDE的周长最小；②共有11个令S△DPE为整数的点．
【解析】（1）设抛物线的解析式为y=a（x+h）2+k
∵点C（0，8）是它的顶点坐标， ∴y=ax2+8
又∵经过点A（8，0），
有64a+8=0，解得a=
故抛物线的解析式为：y=x2+8；
（2）是定值，解答如下：
设P（a，a2+8），则F（a，8），
∵D（0，6），
∴PD=
PF=
，
∴PD﹣PF=2；
（3）当点P运动时，DE大小不变，则PE与PD的和最小时，△PDE的周长最小，
∵PD﹣PF=2，∴PD=PF+2，
∴PE+PD=PE+PF+2，
∴当P、E、F三点共线时，PE+PF最小，
此时点P，E的横坐标都为4，
将x=4代入y=x2+8，得y=6，
∴P（4，6），此时△PDE的周长最小．
过点P做PH⊥x轴，垂足为H．
设P（a，a2+8）
∴PH=a2+8，EH=a-4，OH=a
S△DPE=S梯形PHOD-S△PHE-S△DOE
=
=
=
∵点P是抛物线上点A，C间的一个动点（含端点）
∴0≤a≤8
当a=6时，S△DPE取最大值为13．
当a=0时，S△DPE取最小值为4．
即4≤S△DPE≤13
其中，当S△DPE=12时，有两个点P．
所以，共有11个令S△DPE为整数的点．
