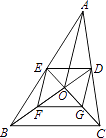��Ŀ����
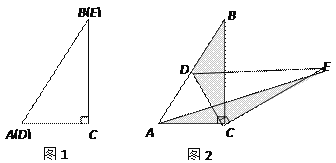
����Ŀ����֪����ABC�ǵ��������Σ�����P��б��AB���ڵ�ֱ���ϣ���PCΪֱ�DZ�������������PCQ�����С�PCQ=90�㣬̽��������������⣺
��1����ͼ�٣�����P���߶�AB�ϣ���AC=1+![]() ��PA=
��PA=![]() ����
����
���߶�PB= ��PC= ��
�ڲ��룺PA2��PB2��PQ2����֮���������ϵΪ ��
��2����ͼ�ڣ�����P��AB���ӳ����ϣ��ڣ�1����������Ľ�����Ȼ��������������ͼ�ڸ���֤�����̣�
��3��������P����![]() ����
����![]() ��ֵ������ʾ�������ñ���ͼ����̽��
��ֵ������ʾ�������ñ���ͼ����̽��
���𰸡���1����![]() ��2����
��2����![]() ����2��֤���������������3��
����2��֤���������������3��![]() ��
��![]() ��
��
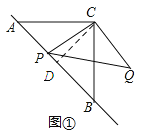
�������������������1�����ڵ���ֱ��������ACB�У������AB�ij���Ȼ�����PA�ij��������PB�ij�������C��CD��AB������ΪD���Ӷ������CD��PD�ij���Ȼ����Rt������CDP�����ݹ��ɶ��������PC�ij����ڡ�ACBΪ����ֱ�������Σ�CD��AB���Ӷ��У�CD=AD=DB��Ȼ�����AP=DC��PD��PB=DC+PD����֤��![]() ����Rt��PCQ�У�
����Rt��PCQ�У�![]() ����ɵó����ۣ�
����ɵó����ۣ�
��2������C��CD��AB������ΪD����AP=��AD+PD��=��DC+PD����PB=��DP��BD��=��PD��DC������֤��![]() ����Ϊ��Rt��PCQ�У�
����Ϊ��Rt��PCQ�У�![]() ����ɵó����ۣ�
����ɵó����ۣ�
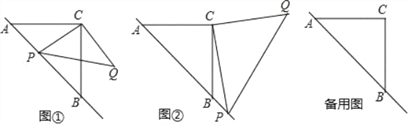
��3�����ݵ�P���ڵ�λ�û���ͼ�Σ�Ȼ��������Ŀ�еı�ֵ��ϵ���PD�ij����ú���CD��ʽ�ӱ�ʾ����Ȼ����Rt��ACP��Rt��DCP���ɹ��ɶ������AC��PC�ij��ȼ��ɣ�
�����������1����ͼ����
�١ߡ�ABC�ǵ���ֱֱ�������Σ�AC=![]() ����AB=
����AB=![]() AC=
AC=![]() ����PA=
����PA=![]() ����PB=
����PB=![]() ����CD��AB��D����AD=CD=
����CD��AB��D����AD=CD=![]() ����PD=AD��PA=
����PD=AD��PA=![]() ����RT��PCD��PC=
����RT��PCD�У�PC=![]() =2���ʴ�Ϊ��
=2���ʴ�Ϊ��![]() ��2��
��2��
����ͼ1���ߡ�ACBΪ����ֱ�������Σ�CD��AB����CD=AD=DB����AP2=��AD��PD��2=��DC��PD��2=DC2��2DCPD+PD2��PB2=��DB+PD��2=��DC+DP��2=CD2+2DCPD+PD2����AP2+BPspan>2=2CD2+2PD2������Rt��PCD�У��ɹ��ɶ�����֪��![]() ����
����![]() ���ߡ�CPQΪ����ֱ�������Σ���
���ߡ�CPQΪ����ֱ�������Σ���![]() ����
����![]() ��
��
��2����ͼ��������C��CD��AB������ΪD��
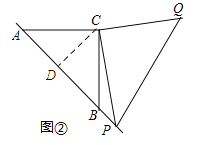
�ߡ�ACBΪ����ֱ�������Σ�CD��AB����CD=AD=DB����AP2=��AD+PD��2=��DC+PD��2=CD2+2DCPD+PD2��PB2=��DP��BD��2=��PD��DC��2=DC2��2DCPD+PD2����AP2+BP2=2CD2+2PD2������Rt��PCD�У��ɹ��ɶ�����֪��![]() ����
����![]() ���ߡ�CPQΪ����ֱ�������Σ���
���ߡ�CPQΪ����ֱ�������Σ���![]() ����
����![]() ��
��
��3����ͼ��������C��CD��AB������ΪD��

������Pλ�ڵ�P1��ʱ����![]() ����
����![]() ����
����![]() ����Rt��CP1D�У��ɹ��ɶ����ã�
����Rt��CP1D�У��ɹ��ɶ����ã�![]() =
=![]() DC����Rt��ACD�У��ɹ��ɶ����ã�AC=
DC����Rt��ACD�У��ɹ��ɶ����ã�AC=![]() =
=![]() =
=![]() DC����
DC���� =
=![]() ��
��
������Pλ�ڵ�P2��ʱ����![]() ����
����![]() ����Rt��CP2D�У��ɹ��ɶ����ã�
����Rt��CP2D�У��ɹ��ɶ����ã�![]() =
=![]() =
=![]() DC����Rt��ACD�У��ɹ��ɶ����ã�AC=
DC����Rt��ACD�У��ɹ��ɶ����ã�AC=![]() =
=![]() =
=![]() DC����
DC����![]() =
=![]() ��
��
����������![]() �ı�ֵΪ
�ı�ֵΪ![]() ��
��![]() ��
��