Question

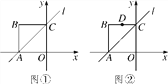
【题目】如图，在平面直角坐标系xOy中，三角板的直角顶点P的坐标为(2，2)，一条直角边与x轴的正半轴交于点A，另一直角边与y轴交于点B，三角板绕点P在坐标平面内转动的过程中，当△POA为等腰三角形时，请写出所有满足条件的点B的坐标__________．

Answer 1

【答案】(0，2)，(0，0)，(0，4－2)

【解析】由P坐标为（2，2），可得∠AOP=45°，然后分别从OA=PA，OP=PA，OA=OP去分析求解即可求得答案．

解：∵P坐标为(2,2)，

∴∠AOP=45°，

①如图1,若OA=PA,则∠AOP=∠OPA=45°，

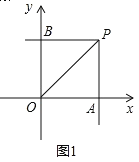
∴∠OAP=90°，

即PA⊥x轴，

∵∠APB=90°，

∴PB⊥y轴，

∴点B的坐标为：(0,2)；

②如图2,若OP=PA,则∠AOP=∠OAP=45°，

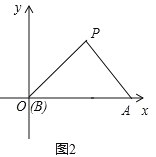
∴∠OPA=90°，

∵∠BPA=90°，

∴点B与点O重合，

∴点B的坐标为(0,0)；

③如图3,若OA=OP,则∠OPA=∠OAP= (180°∠AOP)=67.5°，

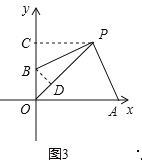
过点P作PC⊥y轴于点C，过点B作BD⊥OP于点D，

则PC∥OA，

∴∠OPC=∠AOP=45°，

∵∠APB=90°，

∴∠OPB=∠APB∠OPA=22.5°，

∴∠OPB=∠CPB=22.5°，

∴BC=BD，

设OB=a，

则BD=BC=2a，

∵∠BOP=45°，

在Rt△OBD中,BD=OBsin45°，

即2a=a，

解得：a=4－2.

综上可得：点B的坐标为：(0,2),(0,0),(0, 4－2).

故答案为：(0,2),(0,0),(0, 4－2).