题目内容
平面直角坐标系中，点A的坐标是（4，0），点P在直线y=-x+m上，且AP=OP=4．求m的值．
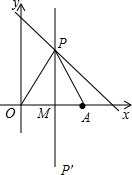
由已知AP=OP，点P在线段OA的垂直平分线PM上．
∴OA=AP=OP=4，
∴△AOP是等边三角形．
如图，当点P在第一象限时，OM=2，OP=4．
在Rt△OPM中，PM=
=
=2
，（4分）
∴P（2，2
）．
∵点P在y=-x+m上，
∴m=2+2
．（6分）
当点P在第四象限时，根据对称性，P′（2，-2
）．
∵点P′在y=-x+m上，
∴m=2-2
．（8分）
则m的值为2+2
或2-2
．
∴OA=AP=OP=4，
∴△AOP是等边三角形．
如图，当点P在第一象限时，OM=2，OP=4．
在Rt△OPM中，PM=
| OP2-OM2 |
| 42-22 |
| 3 |
∴P（2，2
| 3 |
∵点P在y=-x+m上，
∴m=2+2
| 3 |
当点P在第四象限时，根据对称性，P′（2，-2
| 3 |
∵点P′在y=-x+m上，
∴m=2-2
| 3 |
则m的值为2+2
| 3 |
| 3 |
练习册系列答案
相关题目
-3），AC交x轴于点N，BC交y轴于点M，
，且BE⊥AE，连接AB，
，并且OC＞OE．
