Question

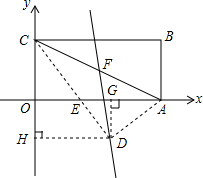
已知：如图，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x轴、y轴的正半轴上，连接AC，将△ABC沿AC翻折，点B落在该坐标平面内，设这个落点为D，CD交x轴于点E．如果CE=5，OC、OE的长是关于x的方程x²+（m-1）x+12=0的两个根，并且OC＞OE．
（1）求点D的坐标；
（2）如果点F是AC的中点，判断点（8，-20）是否在过D、F两点的直线上，并说明现由．

Answer 1

（1）∵OC、OE的长是关于x的方程x²+（m-1）x+12=0的两个根，
设OC=x₁，OE=x₂，x₁＞x₂．
∴x₁+x₂=-（m-1）．x₁•x₂=12．
在Rt△COE中，
∵OC²+OE²=CE²，CE=5．
∴x₁²+x₂²=5²，即（x₁+x₂）²-2x₁x₂=25．
∴[-（m-1）]²-2×12=25，
解这个方程，得m₁=-6，m₂=8．
∵OC+OE=x₁+x₂=-（m-1）＞0，
∴m=8不符合题意，舍去．
∴m=-6．
解方程x²-7x+12=0，得
x₁=4，x₂=3．
∴OC=4，OE=3．
△ABC沿AC翻折后，点B的落点为点D．过D点作DG⊥x轴于G．DH⊥y轴于H．
∴∠BCA=∠ACD．
∵矩形OABC中，CB∥OA．
∴∠BCA=∠CAE．
∴∠CAE=∠ACD．
∴EC=EA．
在Rt△COE与Rt△ADE中，
∵

OC=AD EC=EA

∴Rt△COE≌Rt△ADE．
∴ED=3，AD=4，EA=5．
在Rt△ADE中，DG•AE=ED•AD，
∴DG=

ED•AD

AE

=

12

5

，
在△CHD中，OE∥HD，
∴

CE

CD

=

CE

HD

，

5

5+3

=

3

HD

，
∴HD=

24

5

，
由已知条件可知D是第四象限的点，
∴点D的坐标是（

24

5

，-

12

5

）；

（2）∵F是AC的中点，
∴点F的坐标是（4，2），
设过D、F两点的直线的解析式为y=kx+b．
∴

4k+b=2 24 5 k+b=- 12 5

，解得

k=- 11 2 b=24

，
∴过点D、F两点的直线的解析式为y=-

11

2

x+24，
∵x=8，y=-20满足上述解析式，
∴点（8，-20）在过D、F两点的直线上．