Question

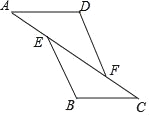
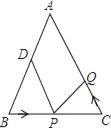
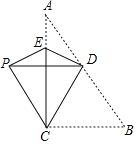
【题目】如图，在△ABC中，∠ACB＝90°，D，E分别为AB，AC上一点，将△BCD，△ADE沿CD，DE翻折，点A，B恰好重合于点P处，若△PCD中有一个角等于50°，则∠A度数等于__．

Answer 1

【答案】40°或25°．

【解析】

由折叠的性质得出AD＝PD＝BD，∠CPD＝∠B，∠PDC＝∠BDC，∠PCD＝∠DCB，由直角三角形斜边上的中线性质得出CD＝AB＝AD＝BD，由等腰三角形的性质得出∠ACD＝∠A，∠DCB＝∠B，然后分三种情况求解即可．

由折叠可得，AD＝PD＝BD，∠CPD＝∠B，∠PDC＝∠BDC，∠PCD＝∠DCB，

∴D是AB的中点，

∴CD＝AB＝AD＝BD，

∴∠ACD＝∠A，∠DCB＝∠B，

当∠CPD＝50°时，∠B＝50°，

∴∠A＝90°﹣∠B＝40°；

当∠PCD＝50°时，∠DCB＝∠B＝50°，

∴∠A＝40°；

当∠PDC＝∠BDC＝50°时，

∵∠BDC＝∠A+∠ACD，

∴∠A＝∠BDC＝25°；

故答案为：40°或25°．