题目内容
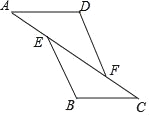
【题目】如图,一次函数y=x+k图象过点A(1,0),交y轴于点B,C为y轴负半轴上一点,且OB=![]() BC,过A,C两点的抛物线交直线AB于点D,且CD∥x轴.
BC,过A,C两点的抛物线交直线AB于点D,且CD∥x轴.
(1)求这条抛物线的解析式;
(2)直接写出使一次函数值小于二次函数值时x的取值范围.

【答案】(1)y=x2+2x﹣3;(2)x<﹣2或x>1
【解析】试题(1)利用待定系数法求解即可得;
(2)结合图象即可进行判断出x的取值范围.
试题解析:(1)把A(1,0)代入y=x+k中,得k=﹣1,
∴y=x﹣1,令x=0,得点B坐标为(0,﹣1),

∵OB=![]() BC,OB=1,∴BC=2,∴OC=3,
BC,OB=1,∴BC=2,∴OC=3,
∴C点坐标为(0,﹣3),
又CD∥x轴,
∴点D的纵坐标为﹣3代入y=x﹣1得x=﹣2,
∴点D的坐标为(﹣2,﹣3),
设抛物线解析式为y=ax2+bx+c,
将A(1,0),C(0,﹣3),D(﹣2,﹣3)代入,得
 ,解得
,解得 ,
,
∴抛物线的解析式为:y=x2+2x﹣3;
(2)∵直线与抛物线交于D(﹣2,﹣3),A(1,0)两点,抛物线开口向上,
∴当x<﹣2或x>1时,一次函数值小于二次函数值.

练习册系列答案
相关题目