题目内容
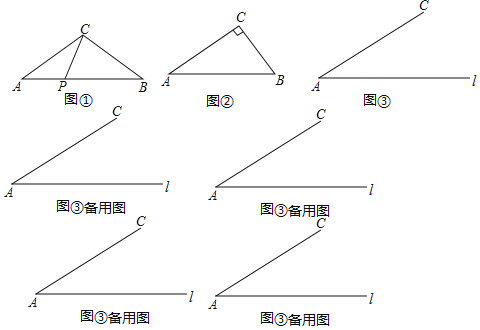
【题目】如图,已知∠MON=90°,点A在射线OM上运动,点B在射线ON上运动,OA>OB,点P在∠MON的平分线上,PA=PB.

(1)∠APB的大小是否发生变化?请说明理由;
(2)连接AB,点E是AB的中点,点F是OP的中点,求证:EF⊥OP.
【答案】(1)∠APB的大小不会变化,理由见解析;(2)见解析
【解析】
(1)过点P作PC⊥AO于C,PD⊥OB于D,由角平分线的性质可得PC=PD,由“HL”可证Rt△ACP≌Rt△BDP,可得∠APC=∠BPD,可求∠APB=90°;
(2)由直角三角形的性质可得OE=PE=![]() AB,由等腰三角形的性质可得EF⊥OP.
AB,由等腰三角形的性质可得EF⊥OP.
解:(1)∠APB的大小不会变化,
理由如下:如图,过点P作PC⊥AO于C,PD⊥OB于D,连接OE,PE,EF,

∵PC⊥AO,PD⊥OB,∠MON=90°,
∴四边形CPDO是矩形,
∴∠CPD=90°,
∵点P在∠MON的平分线上,PC⊥AO,PD⊥OB,
∴PC=PD,且PA=PB,
∴Rt△ACP≌Rt△BDP(HL)
∴∠APC=∠BPD,
∵∠BPC+∠BPD=90°,
∴∠BPC+∠APC=90°,
∴∠APB=90°,
∴∠APB的大小不会变化.
(2)∵点E是AB的中点,∠AOB=∠APB=90°,
∴OE=![]() AB,PE=
AB,PE=![]() AB,
AB,
∴OE=PE,且点F是OP的中点,
∴EF⊥OP

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目