题目内容
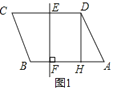
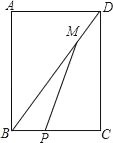
【题目】如图所示，矩形ABCD中，AB＝8，BC＝6，P是线段BC上一点（P不与B重合），M是DB上一点，且BP＝DM，设BP＝x，△MBP的面积为y，则y与x之间的函数关系式为_____．
【答案】y＝
x2+4x（0＜x≤6）．
【解析】
根据勾股定理可得BD=10，因为DM=x，所以BM=10-x，过点M作ME⊥BC于点E，可得到△BME∽△BDC，然后根据相似三角形的性质得到
＝
，由此即可用x表示ME，最后根据三角形的面积公式即可确定函数关系式．
∵AB=8，BC=6，
∴CD=8，
∴BD=10，
∵DM=x，
∴BM=10-x，
如图，
过点M作ME⊥BC于点E，
∴ME∥DC，
∴△BME∽△BDC，
∴＝，
∴ME=8-
x，
而S△MBP=
×BP×ME，
∴y=
x2+4x，P不与B重合，那么x＞0，可与点C重合，那么x≤6．
故答案为：y=x2+4x（0＜x≤6）．
练习册系列答案
轻松暑假总复习系列答案
相关题目
