题目内容
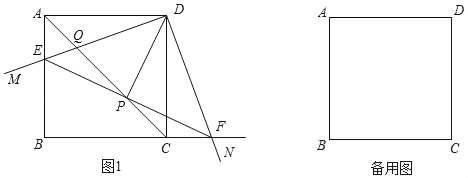
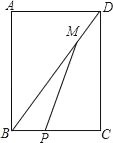
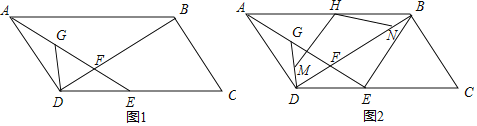
【题目】如图,在平行四边形ABCD中,对角线BD⊥AD,E为CD上一点,连接AE交BD于点F,G为AF的中点,连接DG.
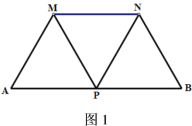
(1)如图1,若DG=DF=1,BF=3,求CD的长;
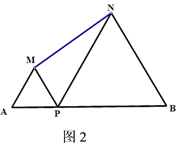
(2)如图2,连接BE,且BE=AD,∠AEB=90°,M、N分别为DG,BD上的点,且DM=BN,H为AB的中点,连接HM、HN,求证:∠MHN=∠AFB.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)由垂直的定义得到∠ADB=90°,根据直角三角形的性质得到DG=GF,根据勾股定理即可得到结论;
(2)连接DH,HE,根据已知条件得到A,D,E,B四点共圆,根据圆周角定理得到∠DHE=2∠DAE,求得∠DGF=2∠DAE,推出∠GDH=∠HEG,根据等腰三角形的性质得到∠EAB=∠ABD,求得∠HBN=∠HDM,根据全等三角形的性质得到∠BHN=∠DHM,得到∠BHD=∠MHN,等量代换即可得到结论.
(1)∵BD⊥AD,
∴∠ADB=90°,
∵G为AF的中点,
∴DG=GF,
∵DG=DF=1,
∴GF=DG=DF=1,
∴AF=2,
∵AD=![]() =
=![]() ,
,
∵BF=3,
∴BD=4,
∴AB=![]() =
=![]() ,
,
∵四边形ABCD是平行四边形,
∴CD=AB=![]() ;
;
(2)连接DH,HE,
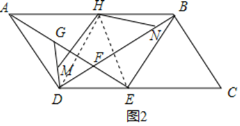
∵AD⊥BD,AE⊥BE,
∴∠ADB=∠AEB=90°,
∵H为AB的中点,
∴DH=BH=EH=AH=![]() AB,
AB,
∵∠ADB=∠AEB=90°,
∴A,D,E,B四点共圆,
∴∠DHE=2∠DAE,
∵AG=DG,
∴∠DGF=2∠DAE,
∴∠DGF=∠DHE,
∴∠GDH=∠HEG,
∵AD=BE,
∴∠EAB=∠ABD,
∵∠EAB=∠AEH,
∴∠HBN=∠AEH,
∴∠HBN=∠HDM,
在△HDM与△HBN中, ,
,
∴△HDM≌△HBN(SAS),
∴∠BHN=∠DHM,
∴∠BHD=∠MHN,
∵∠AFB=180°-∠BAF-∠ABF,
∠DHB=180°-∠HDB-∠HBD,
∴∠AFB=∠DHB,
∴∠MHN=∠AFB.