��Ŀ����
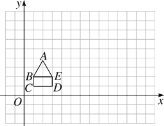
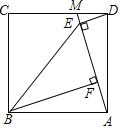
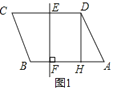
����Ŀ����ͼ1����ABCD�У�DH��AB�ڵ�H��CD�Ĵ�ֱƽ���߽�CD�ڵ�E����AB�ڵ�F��AB=6��DH=4��BF��FA=1��5��
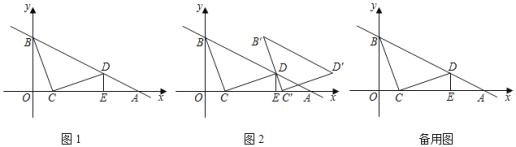
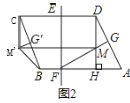
��1����ͼ2����FG��AD�ڵ�G����DH�ڵ�M������DGM��DC����ƽ�ƣ��õ���CG��M��������M��B��
�����ı���BHMM���������
��ֱ��EF����һ����N������DNM�ܳ�����Сֵ��
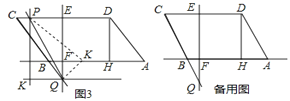
��2����ͼ3���ӳ�CB��EF�ڵ�Q������Q��QK��AB����CD���ϵĶ���P��PK��EF������QK���ڵ�K������PKQ��ֱ��PQ���ۣ�ʹ��K�Ķ�Ӧ��K��ǡ������ֱ��AB�ϣ����߶�CP�ij���
���𰸡���1�����ı���BHMM�������Ϊ7.5������DNM�ܳ�����СֵΪ9����2��CP�ij�Ϊ![]() ��
��![]() ��
��
����������1���ٸ������������ε��ж��������Լ�ƽ�Ƶ����ʽ��н�ɣ�
������CM��ֱ��EF�ڵ�N������DN�����ù��ɶ�����ɣ�
��2���ֵ�P���߶�CE�Ϻ͵�P���߶�ED������������н��
��1������ABCD�У�AB=6��ֱ��EF��ֱƽ��CD��
��DE=FH=3��
��BF��FA=1��5��
��AH=2��
��Rt��AHD��Rt��MHF��
��![]() ��
��
��![]() ��
��
��HM=1.5��
����ƽ�Ƶ����ʣ�MM'=CD=6������BM����ͼ1��
�ı���BHMM�������=![]() =7.5��
=7.5��
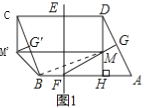
������CM��ֱ��EF�ڵ�N������DN����ͼ2��
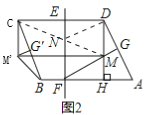
��ֱ��EF��ֱƽ��CD��
��CN=DN��
��MH=1.5��
��DM=2.5��
��Rt��CDM��MC2=DC2+DM2��
��MC2=62+��2.5��2��
��MC=6.5��
��MN+DN=MN+CN=MC��
���DNM�ܳ�����СֵΪ9��
��2����BF��CE��
��![]() ��
��
��QF=2��
��PK=PK'=6��
����K'��E'F'��EF���ֱ�CD�ڵ�E'����QK�ڵ�F'����ͼ3��
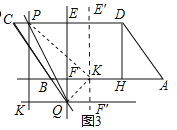
����P���߶�CE��ʱ��
��Rt��PK'E'��
PE'2=PK'2��E'K'2��
��PE��=2![]() ��
��
��Rt��PE'K'��Rt��K'F'Q��
��![]() ��
��
��![]() ��
��
��ã�QF��=![]() ��
��
��PE=PE'��EE'=![]() ��
��
��CP=![]() ��
��
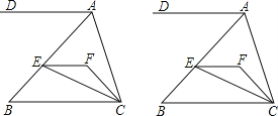
ͬ���ɵã�����P���߶�DE��ʱ��CP��=![]() ������ͼ4��
������ͼ4��

����������CP�ij�Ϊ![]() ��
��![]() ��
��