题目内容
【题目】如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
(1)若AB=4![]() ,求
,求![]() 的长;(结果保留π)
的长;(结果保留π)
(2)求证:四边形ABMC是菱形.
【答案】
(1)
解:∵OA=OB,E为AB的中点,
∴∠AOE=∠BOE,OE⊥AB,
∵OE⊥AB,E为OD中点,
∴OE=![]() OD=
OD=![]() OA,
OA,
∴在Rt△AOE中,∠OAB=30°,∠AOE=60°,∠AOB=120°,
设OA=x,则OE=![]() x,AE=
x,AE=![]() x,
x,
∵AB=4![]() ,
,
∴AB=2AE=![]() x=4
x=4![]() ,
,
解得:x=4,
则![]() 的长l=
的长l=![]() =
=![]() ;
;
(2)
证明:由1得∠OAB=∠OBA=30°,∠BOM=∠COM=60°,∠AMB=30°,
∴∠BAM=∠BMA=30°,
∴AB=BM,
∵BM为圆O的切线,连接OB,如图所示,
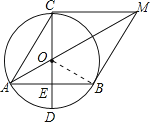
∴OB⊥BM,
在△COM和△BOM中,
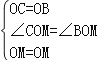 ,
,
∴△COM≌△BOM(SAS),
∴CM=BM,∠CMO=∠BMO=30°,
∴CM=AB,∠CMO=∠MAB,
∴CM∥AB,
∴四边形ABMC为菱形.
【解析】(1)连接OB,由E为OD中点,得到OE等于OA的一半,在直角三角形AOE中,得出∠OAB=30°,进而求出∠AOE与∠AOB的度数,设OA=x,利用勾股定理求出x的值,确定出圆的半径,利用弧长公式即可求出![]() 的长;
的长;
(2)由第一问得到∠BAM=∠BMA,利用等角对等边得到AB=MB,利用SAS得到三角形OCM与三角形OBM全等,利用全等三角形对应边相等得到CM=BM,等量代换得到CM=AB,再利用全等三角形对应角相等及等量代换得到一对内错角相等,进而确定出CM与AB平行,利用一组对边平行且相等的四边形为平行四边形得到ABMC为平行四边形,最后由邻边相等的平行四边形为菱形即可得证.
【考点精析】关于本题考查的菱形的判定方法和切线的性质定理,需要了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案【题目】自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
选项 | 频数 | 频率 |
A | 30 | M |
B | n | 0.2 |
C | 5 | 0.1 |
D | 5 | 0.1 |

(1)这次被抽查的学生有多少人?
(2)求表中m,n的值,并补全条形统计图;
(3)该中学有学生2200名,请估计这餐晚饭有剩饭的学生人数,按平均每人剩10克米饭计算,这餐晚饭将浪费多少千克米饭?