题目内容
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2![]() , AC=3
, AC=3![]() , BC=6,则⊙O的半径是( )
, BC=6,则⊙O的半径是( )
A.3
B.4
C.4![]()
D.2![]()
【答案】D
【解析】解 :延长AC交⊙O于F,连接FD. 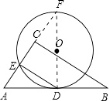
∵∠C=90°,DE∥BC,
∴∠DEF=90°,
∴FD是圆的直径.
∵AB切⊙O于D,
∴FD⊥AB.
∵DE∥BC,
∴△ADE∽△ABC.
∴AE∶AC=DE∶BC,即2∶3=DE∶6,
∴DE=4.
∵∠ADF=90°,DE⊥AF,
∴∠DEF=∠AED=90°;∠A+∠F=90°,∠A+∠ADE=90°;
∴∠F=∠ADE
∴△ADE∽△DFE,
∴DE∶FE=AE∶DE
∴DE2=AEEF,即42= 2![]() EF,
EF,
∴EF=4![]()
∴DF=![]()
OD=![]()
∴半径为![]()
延长AC交⊙O于F,连接FD. 根据二直线平行同旁内角互补得出∠DEF=90°,根据圆周角定理得出FD是圆的直径.根据切线的性质得出FD⊥AB.根据平行于三角形一边的直线截其它两边所截得的三角形与原三角形相似得出△ADE∽△ABC.根据相似三角形对应边成比例得出AE∶AC=DE∶BC,即2∶3=DE∶6,进而得出DE的长度,然后再判断出△ADE∽△DFE,根据相似三角形对应边成比例得出DE∶FE=AE∶DE,即DE2=AEEF,即42= 2EF,算出EF的长度,根据勾股定理得出DF的长度,从而得出该圆的半径。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目