题目内容
【题目】如图,抛物线y=﹣2x2﹣8x﹣6与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1 , 将C1向左平移得C2 , C2与x轴交于点B,D.若直线y=﹣x+m与C1 , C2共有3个不同的交点,则m的取值范围是( )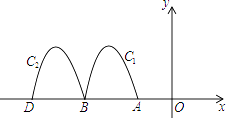
A.﹣3<m<﹣ ![]()
B.![]()
C.﹣2<m< ![]()
D.﹣3<m<﹣2
【答案】A
【解析】解:如图所示:
令y=﹣2x2﹣8x﹣6=0,
即x2+4x+3=0,
解得x=﹣1或﹣3,
则点A(﹣1,0),B(﹣3,0),
由于将C1向左平移2个长度单位得C2 ,
则C2解析式为y=﹣2(x+4)2+2(﹣5≤x≤﹣3),
当y=﹣x+m1与C2相切时,
令y=﹣x+m1=y=﹣2(x+4)2+2,
即2x2+15x+30+m1=0,
△=﹣8m1﹣15=0,
解得m1=﹣ ![]() ,
,
当y=﹣x+m2过点B时,
即0=3+m2 ,
m2=﹣3,
当﹣3<m<﹣ ![]() 时直线y=﹣x+m与C1、C2共有3个不同的交点,
时直线y=﹣x+m与C1、C2共有3个不同的交点,
答案为:A.
数形结合,找好临界点,即找出有两个公共点的情况,然后再平移到有三个交点情况,再继续平移到有两个交点情况,界于两个交点的对应的m之间,就是m的范围.

 互动英语系列答案
互动英语系列答案【题目】研究“掷一枚图钉,钉尖朝上”的概率,两个小组用同一个图钉做试验进行比较,他们的统计数据如下:
掷图钉的次数 | 50 | 100 | 200 | 300 | 400 |
钉尖朝上 的次数 | |||||
第一小组 | 23 | 39 | 79 | 121 | 160 |
第二小组 | 24 | 41 | 81 | 124 | 164 |
(1)请你估计第一小组和第二小组所得的概率分别是多少?
(2)你认为哪一个小组的结果更准确?为什么?
【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下表:
型号 | 进价(元/只) | 售价(元/只) |
| 10 | 12 |
| 15 | 23 |
(1)该店用1300元可以购进![]() ,
,![]() 两种型号的文具各多少只?
两种型号的文具各多少只?
(2)若把(1)中所购进![]() ,
,![]() 两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共![]() 个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数 |
|
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
|
摸到白球的频率 |
|
|
|
|
|
|
|
![]() 请估计:当实验次数为
请估计:当实验次数为![]() 次时,摸到白球的频率将会接近________;(精确到
次时,摸到白球的频率将会接近________;(精确到![]() )
)
![]() 假如你摸一次,你摸到白球的概率
假如你摸一次,你摸到白球的概率![]() (摸到白球)
(摸到白球)![]() ________;
________;
![]() 如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为
如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为![]() ?
?