题目内容
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先解方程组![]() 得P点坐标为(3a﹣1,4a+2),则可确定点P为直线y=
得P点坐标为(3a﹣1,4a+2),则可确定点P为直线y=![]() x+
x+![]() 上一动点,设直线y=
上一动点,设直线y=![]() x+
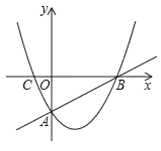
x+![]() 与坐标的交点为A、B,如图,则A(﹣
与坐标的交点为A、B,如图,则A(﹣![]() ,0),B(0,
,0),B(0,![]() ),利用勾股定理计算出AB=
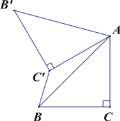
),利用勾股定理计算出AB=![]() ,过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,证Rt△MBP∽Rt△ABO,利用相似比计算出MP=
,过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小,证Rt△MBP∽Rt△ABO,利用相似比计算出MP=![]() ,则PQ=
,则PQ=![]() ,即线段PQ的最小值为
,即线段PQ的最小值为![]() .
.
解方程组![]() 得
得![]() ,
,
∴P点坐标为(3a﹣1,4a+2),
设x=3a﹣1,y=4a+2,
∴y=![]() x+
x+![]() ,
,
即点P为直线y=![]() x+
x+![]() 上一动点,
上一动点,
设直线y=![]() x+
x+![]() 与坐标的交点为A、B,如图,则A(﹣
与坐标的交点为A、B,如图,则A(﹣![]() ,0),B(0,
,0),B(0,![]() ),
),
∴AB=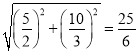
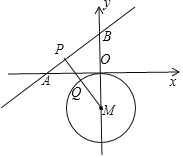
过M点作MP⊥直线AB于P,交⊙M于Q,此时线段PQ的值最小.
∵∠MBP=∠ABO,
∴Rt△MBP∽Rt△ABO,
∴MP:OA=BM:AB,即MP:![]() =
=![]() :
:![]() ,
,
∴MP=![]() ,∴PQ=
,∴PQ=![]() ﹣1=
﹣1=![]() ,
,
即线段PQ的最小值为![]() .
.
故选:C.

练习册系列答案
相关题目