题目内容
【题目】如图所示,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕着点B逆时针旋转60,得到△BAE,连接ED,则下列结论中:①AE∥BC;②∠DEB=60;③∠ADE=∠BDC,其中正确结论的序号是( )
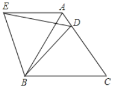
A.①②B.①③C.②③D.只有①
【答案】A
【解析】
由旋转的性质和等边三角形的性质易证∠BAE=∠ABC,,即可得AE∥BC,①正确;证明△BDE是等边三角形,可得②正确; 根据已知条件不能够证明③正确.
∵△ABC为等边三角形,
∴∠ABC=∠C=60°.
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠C=60°.
∴∠BAE=∠ABC,
∴AE∥BC,
所以①正确;
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠DBE=60°,BD=BE.
∴△BDE为等边三角形,
∴∠DEB=60;
所以②正确.
根据已知条件不能够证明③正确.
故选A.

练习册系列答案
相关题目