题目内容
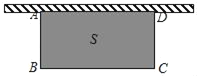
【题目】如图.利用一面墙(墙的长度不限),用20m的篱笆围成一个矩形场地ABCD.设矩形与墙垂直的一边AB=xm,矩形的面积为Sm2.
(1)用含x的式子表示S;
(2)若面积S=48m2,求AB的长;
(3)能围成S=60m2的矩形吗?说明理由.
【答案】(1)S=x(20﹣2x) (2)4m或6m (3)答案见解析
【解析】
(1)靠墙的一面不需要篱笆,矩形养鸡场只需要一个长,两个宽用篱笆围成.设宽为xm,长就是(20-2x)m,用矩形面积公式列表示出S;
(2)令s=48,求得x的值即可;
(3)令s=60,利用根的判别式判断即可;
解:(1)设矩形与墙垂直的一边AB=xm,矩形的面积为Sm2,则长为(20﹣2x)(m);
依题意列方程:
根据题意得到:S=x(20﹣2x)
(2)x(20﹣2x)=48,
解得x=4或x=6,
故AB的长为4m或6m.
(3)不能.
因为设矩形场地的宽为x(m),则长为(20﹣2x)(m),
依题意列方程:x(20﹣2x)=60,
即x2﹣10x+30=0,
△=102﹣4×1×30=﹣20<0,
方程无实数解,
故矩形场地的面积不能达到60m2

练习册系列答案
相关题目