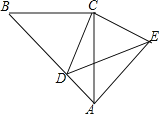
题目内容
【题目】如图1，在
中，
，点
为
边上一点，连接BD，点
为
上一点，连接
，
，过点
作
，垂足为
，交
于点
．
(1)求证：
；
(2)如图2，若
，点为的中点，求证：
；
(3)在(2)的条件下，如图3，若
，求线段
的长．
【答案】（1）详见解析；（2）详见解析；（3）6
【解析】
（1）根据直角三角形的性质可得
，
，然后根据三角形的内角和和已知条件即可推出结论；
（2）根据直角三角形的性质和已知条件可得
，进而可得
，
，然后即可根据AAS证明
≌
，可得
，进一步即可证得结论；
（3）连接
，过点
作
交
延长线于点
，连接
，如图4．先根据已知条件、三角形的内角和定理和三角形的外角性质推出
，进而可得
，然后即可根据SAS证明△ABE≌△ACH，进一步即可推出
，过点
作
于K，易证△AKD≌△CHD，可得
，然后即可根据等腰三角形的性质推得DF=2EF，问题即得解决．
（1）证明：如图1，
，
，
，
，
，
，
，
；
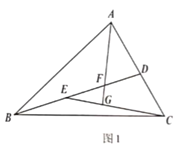
（2）证明：如图2，
，，
，
，
，，
∵点
为
的中点，∴AD=CD，
，
≌（AAS），
，
，
；
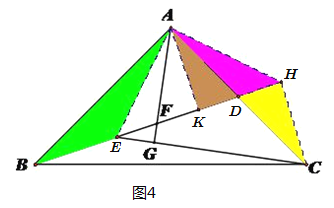
（3）解：连接，过点作交延长线于点，连接，如图4．
，
，
设
，则
，
，
，
，
，
，
，∴△ABE≌△ACH（SAS），
，
，
过点作于K，
，
，
，
∴△AKD≌△CHD（AAS），
，
∵
，
，
，
．
阅读快车系列答案【题目】受气候的影响，某超市蔬菜供应紧张，需每天从外地调运蔬菜1000斤．超市决定从甲、乙两大型蔬菜棚调运蔬菜，已知甲蔬菜棚每天最多可调出800斤，乙蔬菜棚每天最多可调运600斤，从两蔬菜棚调运蔬菜到超市的路程和运费如下表：
到超市的路程（千米） | 运费（元/斤·千米） | |
甲蔬菜棚 | 120 | 0.03 |
乙蔬菜棚 | 80 | 0.05 |
（1）若某天调运蔬菜的总运费为3840元，则从甲、乙两蔬菜棚各调运了多少斤蔬菜？
（2）设从甲蔬菜棚调运蔬菜
斤，总运费为
元，试写出与的函数关系式，怎样安排调运方案才能使每天的总运费最省？
【题目】某高科技产品开发公司现有员工50名，所有员工的月工资情况如下表：
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数（名） | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资（元） | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容，解答下列问题：
（1）该公司“高级技工”有 名；
（2）所有员工月工资的平均数x为2500元，中位数为 元，众数为 元；
（3）小张到这家公司应聘普通工作人员．请你回答右图中小张的问题，并指出用（2）中的哪个数据向小张介绍员工的月工资实际水平更合理些；
（4）去掉四个管理人员的工资后，请你计算出其他员工的月平均工资
（结果保留整数），并判断能否反映该公司员工的月工资实际水平．
