Question

【题目】(1)问题发现

如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．填空：

①∠AEB的度数为______；

②线段AD，BE之间的数量关系为______．

(2)拓展探究

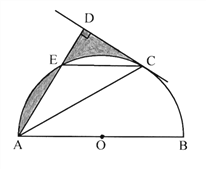
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

Answer 1

【答案】结论：（1）60；（2）AD=BE；应用：∠AEB＝90°；AE=2CM+BE；

【解析】

试题探究：（1）通过证明△CDA≌△CEB，得到∠CEB=∠CDA=120°，又∠CED=60°，∴∠AEB=120°－ 60°= 60°；

（2）已证△CDA≌△CEB，根据全等三角形的性质可得AD=BE；

应用：通过证明△ACD≌△BCE，得到AD = BE，∠BEC = ∠ADC=135°，所以∠AEB =∠BEC－∠CED =135°－ 45°= 90°；根据等腰直角三角形的性质可得DE = 2CM，所以AE = DE+AD=2CM+BE．

试题解析：解：探究：（1）在△CDA≌△CEB中，

AC=BC，∠ACD=∠BCE，CD=CE，

∴△CDA≌△CEB，

∴∠CEB=∠CDA=120°，

又∠CED=60°，

∴∠AEB=120°－ 60°= 60°；

（2）∵△CDA≌△CEB，

∴AD=BE；

应用：∠AEB＝90°；AE=2CM+BE；

理由：∵△ACB和△DCE均为等腰直角三角形，∠ACB =∠DCE= 90°，

∴AC = BC， CD = CE， ∠ACB =∠DCB =∠DCE－∠DCB， 即∠ACD = ∠BCE，

∴△ACD≌△BCE，

∴AD = BE，∠BEC = ∠ADC=135°．

∴∠AEB =∠BEC－∠CED =135°－ 45°= 90°．

在等腰直角三角形DCE中，CM为斜边DE上的高，

∴CM =" DM" = ME，∴DE = 2CM．

∴AE = DE+AD=2CM+BE．