题目内容
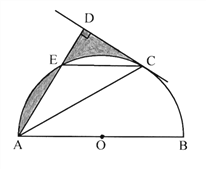
【题目】小明手上一张扇形纸片OAB．现要求在纸片上截一个正方形，使它的面积尽可能大．
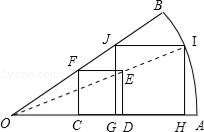
小明的方案是：如图，在扇形纸片OAB内，画正方形CDEF，使C、D在OA上，F在OB上；连接OE并延长交弧AB于I，画IH∥ED交OA于H，IJ∥OA交OB于J，再画JG∥FC交OA于G．
（1）你认为小明画出的四边形GHIJ是正方形吗？如果是，请证明．如果不是，请说明理由．
（2）如果扇形OAB的圆心角∠AOB=30°，OA=6cm，小明截得的四边形GHIJ面积是多少（结果精确到0.1cm）．
（3）（1）中小明画出的四边形GHIJ如果是正方形，我们把它叫做扇形的内接正方形（四个顶点分别在扇形的半径和弧上）．请你再画出一种不同于图（1）的扇形的内接正方形（保留画图痕迹，不要求证明）
【答案】（1）是，详见解析；（2）正方形GHIJ的面积是4.3cm2；（3）详见解析.
【解析】试题分析：（1）根据HI∥DE，JG∥FC，JI∥GH，利用矩形的判定得出四边形JGHI是矩形，进而利用平行线分线段成比例定理得出即可；
（2）正方形GHIJ的边长为x，则GH=HI=JG=x，表示出GO= 
， 
，再利用勾股定理求解；
（3）画一个使正方形一边平行于AB的一个正方形即可．
（1）答：是．
证明：∵在扇形纸片OAB内，画正方形CDEF，IH∥ED交OA于H，
IJ∥OA交OB于J，JG∥FC交OA于G，
∴HI∥DE，JG∥FC，JI∥GH，
∴∠JGH=∠IHG=∠JIH=90°，
∴四边形JGHI是矩形，
∵HI∥DE，JG∥FC，JI∥GH，
∴
，
，
∴
，
∵FE=DE，
∴JI=HI，
∴矩形JGHI是正方形，
（2）设正方形GHIJ的边长为x，则GH=HI=JG=x，
∵∠AOB=30°，OA=6cm，
在直角三角形△OGJ，∠GOJ=30°，
∴GO=
x，
∴HO=x+x，
∴
，
x2=
≈4.3，
所以正方形GHIJ的面积是4.3cm2．
（3）如图：
