题目内容
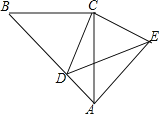
【题目】如图,△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,且点D在线段AB上,连接AE.
(1)求证:①△BCD≌△ACE;②∠DAE=90°;
(2)若AB=8,当点D在线段AB上什么位置时,四边形ADCE的周长最小?请说明并求出周长的最小值.
【答案】(1)①详见解析;②90°;(2)点D是AB中点时,四边形ADCE的周长最小,最小值为16.
【解析】
![]() 判断出
判断出![]() ,
,![]() ,
,![]() ,即可得出结论;
,即可得出结论;![]() 利用全等三角形的性质得出
利用全等三角形的性质得出![]() ,即可得出结论;
,即可得出结论;![]() 先判断出
先判断出![]() ,进而判断出
,进而判断出![]() 时,CD最小,即可得出结论.
时,CD最小,即可得出结论.
(1)证明:①∵△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,
∴BC=AC,CD=CE,∠BCD=∠ACE.
在△BCD和△ACE中,
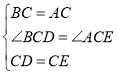 ,
,
∴△BCD≌△ACE(SAS);
②∵△ABC是等腰直角三角形,
∴∠ABC=∠BAC=45°,
由①知,△BCD≌△ACE,
∴∠ABC=∠EAC,
∴∠DAE=∠DAC+∠CAE=45°+45°=90°;
(2)∵△CDE是等腰直角三角形,
∴CD=CE,
由(1)知,△BCD≌△ACE,
∴BD=AE,
∴l四边形ADCE=AD+AE+CE+CD=AB+2CD=8+2CD,
要四边形ADCE的周长最小,
∴CD最小,
∵点D在AB上,
∴CD⊥AB时,CD最小,
∵AC=BC,
∴AD=BD.
即:点D是AB的中点,
∵△ABC是等腰直角三角形,AB=8,
∴CD最小=4,
∴l四边形ADCE最小=8+2CD最小=8+2×4=16,
即:点D是AB中点时,四边形ADCE的周长最小,最小值为16.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目