题目内容
在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C ,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连接CD,求∠OCA与∠OCD两角和的度数.
 ,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连接CD,求∠OCA与∠OCD两角和的度数.
(1)∵y=kx沿y轴向上平移3个单位长度后经过y轴上的点C,
∴C(0,3).
设直线BC的解析式为y=kx+3.
∵B(3,0)在直线BC上,
∴3k+3=0.
解得k=-1.
∴直线BC的解析式为y=-x+3.(1分)
∵抛物线y=x2+bx+c过点B,C,
∴
解得
,
∴抛物线的解析式为y=x2-4x+3.(2分)
(2)由y=x2-4x+3.
可得D(2,-1),A(1,0).
∴OB=3,OC=3,OA=1,AB=2.
可得△OBC是等腰直角三角形,
∴∠OBC=45°,CB=3
.
如图1,设抛物线对称轴与x轴交于点F,
∴AF=
AB=1.
过点A作AE⊥BC于点E.
∴∠AEB=90度.
可得BE=AE=
,CE=2
.
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.
∴
=
,
=
.
解得PF=2.∵点P在抛物线的对称轴上,
∴点P的坐标为(2,2)或(2,-2).(5分)

(3)解法一:
如图2,作点A(1,0)关于y轴的对称点A',则A'(-1,0).
连接A'C,A'D,
可得A'C=AC=
,∠OCA'=∠OCA.
由勾股定理可得CD2=20,A'D2=10.
又∵A'C2=10,
∴A'D2+A'C2=CD2.
∴△A'DC是等腰直角三角形,∠CA'D=90°,
∴∠DCA'=45度.
∴∠OCA'+∠OCD=45度.
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.(7分)
解法二:
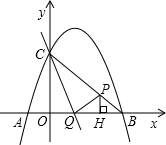
如图3,连接BD.
同解法一可得CD=
,AC=
.
在Rt△DBF中,∠DFB=90°,BF=DF=1,
∴DB=
=
.
在△CBD和△COA中,
=
=
,
=
=
,
=
=
.
∴
=
=
.
∴△CBD∽△COA.
∴∠BCD=∠OCA.
∵∠OCB=45°,
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.(9分)

∴C(0,3).
设直线BC的解析式为y=kx+3.
∵B(3,0)在直线BC上,
∴3k+3=0.
解得k=-1.
∴直线BC的解析式为y=-x+3.(1分)
∵抛物线y=x2+bx+c过点B,C,
∴
|
解得
|
∴抛物线的解析式为y=x2-4x+3.(2分)
(2)由y=x2-4x+3.
可得D(2,-1),A(1,0).
∴OB=3,OC=3,OA=1,AB=2.
可得△OBC是等腰直角三角形,
∴∠OBC=45°,CB=3
| 2 |
如图1,设抛物线对称轴与x轴交于点F,
∴AF=
| 1 |
| 2 |
过点A作AE⊥BC于点E.
∴∠AEB=90度.
可得BE=AE=
| 2 |
| 2 |
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.
∴
| AE |
| AF |
| CE |
| PF |
| ||
| 1 |
2
| ||
| PF |
解得PF=2.∵点P在抛物线的对称轴上,
∴点P的坐标为(2,2)或(2,-2).(5分)

(3)解法一:
如图2,作点A(1,0)关于y轴的对称点A',则A'(-1,0).
连接A'C,A'D,
可得A'C=AC=
| 10 |
由勾股定理可得CD2=20,A'D2=10.
又∵A'C2=10,
∴A'D2+A'C2=CD2.
∴△A'DC是等腰直角三角形,∠CA'D=90°,
∴∠DCA'=45度.
∴∠OCA'+∠OCD=45度.
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.(7分)
解法二:

如图3,连接BD.
同解法一可得CD=
| 20 |
| 10 |
在Rt△DBF中,∠DFB=90°,BF=DF=1,
∴DB=
| DF2+BF2 |
| 2 |
在△CBD和△COA中,
| DB |
| AO |
| ||
| 1 |
| 2 |
| BC |
| OC |
3
| ||
| 3 |
| 2 |
| CD |
| CA |
| ||
|
| 2 |
∴
| DB |
| AO |
| BC |
| OC |
| CD |
| CA |
∴△CBD∽△COA.
∴∠BCD=∠OCA.
∵∠OCB=45°,
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.(9分)


练习册系列答案
相关题目
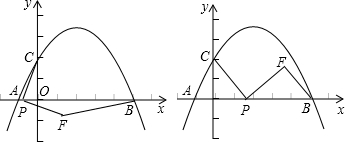



 0,3)的直线y=-
0,3)的直线y=-