题目内容
松花江大桥的一个桥拱为抛物线形状，拱顶A离桥面50m，桥面上拱形钢梁之间的距离BC=120m，建立如图所示的直角坐标系．
（1）写出A，B，C三点的坐标；
（2）求该抛物线的解析式．
（1）写出A，B，C三点的坐标；
（2）求该抛物线的解析式．
由题意得，OA=50m，OB=OC=
BC=60m，
∴A（0，50），B（-60，0），C（60，0）；
（2）设抛物线解析式为：y=ax2+c，
将点A、B的坐标代入可得：
，
解得：
，
故该抛物线的解析式为：y=-
x2+50．
| 1 |
| 2 |
∴A（0，50），B（-60，0），C（60，0）；
（2）设抛物线解析式为：y=ax2+c，
将点A、B的坐标代入可得：
|
解得：
|
故该抛物线的解析式为：y=-
| 1 |
| 72 |
练习册系列答案
中考解读考点精练系列答案
相关题目
线与x轴的另一个交点．
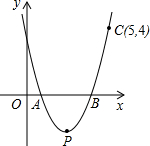
60°．飞机继续飞行0.1千米到达E处进行空投，已知空投物资在空中下落过程中的轨迹是抛物线，若要使空投物资刚好落在O处．
