题目内容
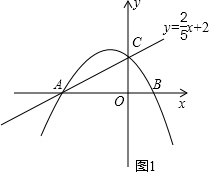
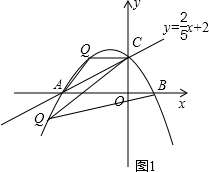
如图1,已知直线y=
x+2与x轴交于点A,交y轴于C、抛物线y=ax2+4ax+b经过A、C两点,抛物线交x轴于另一点B.
(1)求抛物线的解析式;
(2)点Q在抛物线上,且有△AQC和△BQC面积相等,求点Q的坐标;
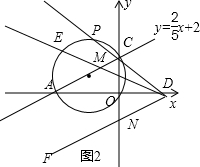
(3)如图2,点P为△AOC外接圆上
的中点,直线PC交x轴于D,∠EDF=∠ACO.当∠EDF绕D旋转时,DE交AC于M,DF交y轴负半轴于N、问CN-CM的值是否发生变化?若不变,求出其值;若变化,求出变化范围.
| 2 |
| 5 |
(1)求抛物线的解析式;
(2)点Q在抛物线上,且有△AQC和△BQC面积相等,求点Q的坐标;
(3)如图2,点P为△AOC外接圆上
 |
| ACO |


(1)由直线AC的解析式可得:A(-5,0),C(0,2);
代入抛物线的解析式中可得:
,
解得
;
故抛物线的解析式为:y=-
x2-
x+2.
(2)易知B(1,0);
①当Q在AC段的抛物线上时,
△ACQ和△BCQ同底,若它们的面积相等,则A、B到直线CQ得距离相等,即CQ∥AB;
由于抛物线的对称轴为x=-2,
故Q(-4,2);
②当Q在线段AC外的直线上时,
△ACQ的面积为:
AL•|yC-yQ|,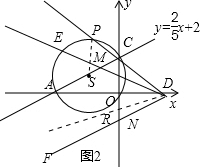
△BCQ的面积为:
BL•|yC-yQ|,
若两个三角形的面积相等,
那么AL=BL,
即L是线段AB的中点,即L(-2,0);
易知直线CL的解析式为:y=x+2,联立抛物线的解析式得:
,
解得
,
;
故Q(-
,-
);
综上所述,存在两个符合条件的点Q,且坐标为:Q(-4,2)或(-
,-
).
(3)如图,设△AOC的外接圆圆心为S;
作∠NDR=∠PDE,交y轴于R;
则∠PDR=∠MDN=∠ACO;
由于P点是
的中点,由垂径定理知SP必平行于y轴,得:
∠PSC=∠ACO=∠CDR,∠SPC=∠RCD;
则△SCP∽△DCR,
所以△CDR也是等腰三角形;
即CD=DR,OC=OR;
∵∠PCS=∠DRC,
∴∠DCM=∠DRN,
又∵∠CDM=∠NDR,CD=DR,
∴△DCM≌△DRN,
得CM=RN,
故CN-CM=CR=2OC;
所以CN-CM的值不变,恒为2OC,即4.
代入抛物线的解析式中可得:
|
解得
|

故抛物线的解析式为:y=-
| 2 |
| 5 |
| 8 |
| 5 |
(2)易知B(1,0);
①当Q在AC段的抛物线上时,
△ACQ和△BCQ同底,若它们的面积相等,则A、B到直线CQ得距离相等,即CQ∥AB;
由于抛物线的对称轴为x=-2,
故Q(-4,2);
②当Q在线段AC外的直线上时,
△ACQ的面积为:
| 1 |
| 2 |

△BCQ的面积为:
| 1 |
| 2 |
若两个三角形的面积相等,
那么AL=BL,
即L是线段AB的中点,即L(-2,0);
易知直线CL的解析式为:y=x+2,联立抛物线的解析式得:
|
解得
|
|
故Q(-
| 13 |
| 2 |
| 9 |
| 2 |
综上所述,存在两个符合条件的点Q,且坐标为:Q(-4,2)或(-
| 13 |
| 2 |
| 9 |
| 2 |
(3)如图,设△AOC的外接圆圆心为S;
作∠NDR=∠PDE,交y轴于R;
则∠PDR=∠MDN=∠ACO;
由于P点是
 |
| ACO |
∠PSC=∠ACO=∠CDR,∠SPC=∠RCD;
则△SCP∽△DCR,
所以△CDR也是等腰三角形;
即CD=DR,OC=OR;
∵∠PCS=∠DRC,
∴∠DCM=∠DRN,
又∵∠CDM=∠NDR,CD=DR,
∴△DCM≌△DRN,
得CM=RN,
故CN-CM=CR=2OC;
所以CN-CM的值不变,恒为2OC,即4.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目