题目内容
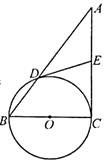
【题目】如图是某小区的一个健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
【答案】解:过点A作AE⊥CD于点E,过点B作BF⊥AE于点F,
∵OD⊥CD,∠BOD=70°,∴AE//OD,∴∠A=∠BOD=70°,
在Rt△AFB中,AB=2.7,∴AF=2.7cos70°=2.7×0.34=0.918,
∴AE=AF+BC=0.918+0.15=1.068≈1.1(m).
答:端点A到地面CD的距离约是1.1m.
【解析】求求端点A到地面CD的距离,则可过点A作AE⊥CD于点E,在构造直角三角形,可过点B作BF⊥AE于点F,即在Rt△AFB中,AB已知,且∠A=∠BOD=70°,即可求出AF的长,则AE=AF+EF即可求得答案.

练习册系列答案
相关题目