题目内容
【题目】将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1 , B1C1交CD于点E,AB= ![]() ,则四边形AB1ED的内切圆半径为( )
,则四边形AB1ED的内切圆半径为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1 ,
则∠OAF=30°,∠AB1O=45°,
故B1F=OF= ![]() OA,
OA,
设B1F=x,则AF= ![]() ﹣x,
﹣x,
故( ![]() ﹣x)2+x2=(2x)2 ,
﹣x)2+x2=(2x)2 ,
解得x= ![]() 或x=
或x= ![]() (舍去),
(舍去),
∴四边形AB1ED的内切圆半径为: ![]() .
.
故选:B.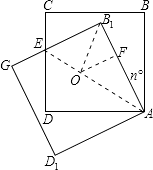
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对三角形的内切圆与内心的理解,了解三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目