题目内容
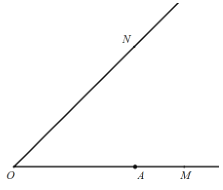
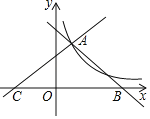
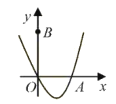
【题目】如图,在平面直角坐标系中,![]() 为坐标原点.抛物线
为坐标原点.抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是该抛物线第一象限图像上的一点,
是该抛物线第一象限图像上的一点,![]() 三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点
三点均在某一个正方形的边上,且该正方形的任何一条边均与某条坐标轴平行,设点![]() 的横坐标为
的横坐标为![]() .若这个正方形的面积最小,则
.若这个正方形的面积最小,则![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]()
【解析】
根据抛物线![]() 与x轴正半轴交于点A,得点A坐标为(2,0),点B的坐标为(0,3),可得最小正方形的边长为3,最小正方形的面积为9,根据题意可得A、B、C中任意两个点不能重合,故此可以确定点C的横坐标的取值范围.
与x轴正半轴交于点A,得点A坐标为(2,0),点B的坐标为(0,3),可得最小正方形的边长为3,最小正方形的面积为9,根据题意可得A、B、C中任意两个点不能重合,故此可以确定点C的横坐标的取值范围.
解:∵抛物线![]() 与x轴正半轴交于点A,
与x轴正半轴交于点A,
∴点A的坐标为(2,0),
如图所示:
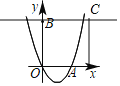
当A,B,C三点均在某一个正方形的边上, 且该正方形的任何一条边均与某条坐标轴平行,
∵点B的坐标为(0,3), 正方形的面积最小时, 此时正方形的边长为3,
∴过点A、B、C的正方形的面积最小值为9,
∴S≥9.
当y=3时,![]() 解得
解得![]()
∴当2<m≤3,时, 正方形面积有最小值;
当m=-1时, 正方形最小边长也为3, 正方形面积也有最小值,
∵C在第一象限,m>0,
综上所述:点C的横坐标m的取值范围是: 2<m≤3.
故答案为:2<m≤3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
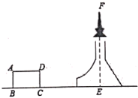
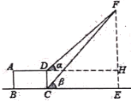
【题目】下表是小安填写的数学实践活动报告的部分内容
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)