题目内容
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
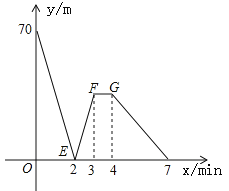
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.
①当3≤x≤4时,甲机器人的速度为____m/min;
②直接写出两机器人出发多长时间相距28m.
【答案】(1)70;490;95;(2)y=35x-70;(3)①60;②两机器人出发1.2min、2.8min或4.6min时相距28m.
【解析】
(1)根据图象可直接读出A、B两点间的距离;A、C两点间的距离=A、B两点间的距离+B、C两点间的距离,代入计算即得;先求出甲在2分钟所走的路程=70+60×2,根据速度=路程÷时间,即可求出a.
(2)结合(1)中数据,计算1×(95-60)=35,所以可得点F(3,35),设线段EF所在直线的函数解析式为y=kx+b,然后将点E、F坐标代入解析式中,解出k 、b的值即得.
(3)①由线段FG∥x轴,可得在FG这段时间内甲、乙的速度相等,即得3≤x≤4时的速度.
②分三种情况讨论:当0≤x≤2时,根据70-甲行路程+乙行路程=28列出方程,解出即得;当2<x≤3时,甲行路程-70-乙行路程=28列出方程,解出即得;当4<x≤7时,先求出直线EF的解析式,然后令y=28,解出x即得.
解:(1)由图象,得A、B两点之间的距离是70m,A、C两点间的距离为70+60×7=490(m),a=(70+60×2)÷2=95(m/min).
故答案为70;490;95.
(2)解:由题意,得点F的坐标为(3,35),设线段EF所在直线的函数解析式为y=kx+b,把E、F的坐标代入解析式,可得 ![]() ,
,
解得 ![]() ,
,
即线段EF所在直线的函数解析式是y=35x-70.
(3)①线段FG∥x轴,
∴在FG这段时间内甲、乙的速度相等,
∴当3≤x≤4时,甲机器人的速度为60m/min.
②当0≤x≤2时,则70-(95-60)x=28,得x=1.2;
当2<x≤3时,则95x-70-60x=28,得x=2.8;
当4<x≤7时,设甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间函数关系式为y=mx+n,  ,
,
即y=-![]() x+
x+![]() ,
,
令y=28,得28=-![]() x+
x+![]() ,解得x=4.6,
,解得x=4.6,
答:两机器人出发1.2min、2.8min或4.6min时相距28m.