题目内容
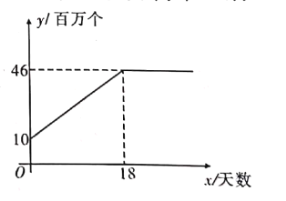
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
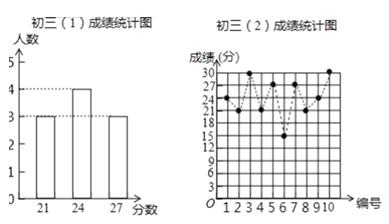
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | ________ | 5.4 |
初三(2)班 | 24 | _________ | 21 | ________ |
(2)哪个班的学生纠错的得分更稳定?若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)现从两个班抽取了数学成绩最好的甲、乙、丙、丁四位同学,并随机分成两组进行数学竞赛,求恰好选中甲、乙一组的概率.
【答案】(1)24,24,![]() ;(2)初三(1)班纠错的得分更稳定;两班各有28、24人成绩优秀;(3)
;(2)初三(1)班纠错的得分更稳定;两班各有28、24人成绩优秀;(3)![]() .
.
【解析】
(1)根据方差、中位数和众数的定义进行解答即可;
(2)根据方差判断稳定性,找到样本中24分和24分以上人数所占的比值,用样本平均数估计总体平均数;
(3)通过画树状图或列表即可求出概率.
解:(1)初三(1)班有4名学生24分,最多,故众数为24,
把初三(2)班的成绩从小到大排列,则处于中间位置的数为24和24,故中位数为24分,
初三(2)班成绩的方差为
![]() ;
;
将数据填入表中为
班级 | 平均数/分 | 中位数/分 | 众数/分 | 方差/分 |
初三(1)班 | 24 | 24 | 24 | 5.4 |
初三(2)班 | 24 | 24 | 21 | 19.8 |
(2)∵5.4<19.8,初三(1)班成绩的方差小,
∴初三(1)班纠错的得分更稳定;
初三(1)班成绩优秀人数为![]() (人),
(人),
初三(2)班成绩优秀人数为![]() (人);
(人);
(3)根据题意画树状图如下: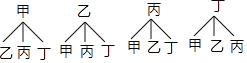
∵共有12种等可能的结果,甲、乙分在同一组的有2种情况,
∴甲、乙分在同一组的概率为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下表是小安填写的数学实践活动报告的部分内容
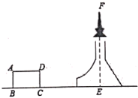
题 目 | 测量铁塔顶端到地面的高度 | |
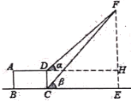
测量目标示意图 |
|
|
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)