题目内容
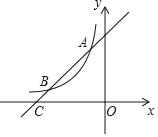
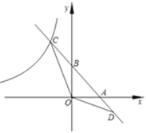
【题目】如图,直线y=﹣x+2与x轴交于点A,与y轴交于点B,与反比例函数![]() (x<0)的图象交于点C,点D(3,a)在直线y=﹣x+2上,连接OD,OC,若∠COD=135°,则k的值为( )
(x<0)的图象交于点C,点D(3,a)在直线y=﹣x+2上,连接OD,OC,若∠COD=135°,则k的值为( )
A. ﹣2 B. ﹣4 C. ﹣6 D. ﹣8
【答案】D
【解析】
作CH⊥y轴于H,如图,先利用一次函数解析式确定B(0,2)、A(2,0),D(3,-1),则AD=![]() ,再证明△OAB为等腰直角三角形得到∠OAB=∠ABO=45°,接着证明△OBC∽△DAO,则利用相似比得到BC=2
,再证明△OAB为等腰直角三角形得到∠OAB=∠ABO=45°,接着证明△OBC∽△DAO,则利用相似比得到BC=2![]() ,于是利用△BCH为等腰直角三角形求出CH=BH=
,于是利用△BCH为等腰直角三角形求出CH=BH=![]() BC=2,从而得到C(-2,4),然后根据反比例函数图象上点的坐标确定k的值.
BC=2,从而得到C(-2,4),然后根据反比例函数图象上点的坐标确定k的值.
解:作CH⊥y轴于H,如图,

当x=0时,y=-x+2=2,则B(0,2);
当y=0时,-x+2=0,解得x=2,则A(2,0),
当x=3时,y=-x+2=-1,则D(3,-1),
∴AD=![]() =
=![]() ,
,
∵OA=OB,
∴△OAB为等腰直角三角形,
∴∠OAB=∠ABO=45°,
∴∠OBC=∠OAD=135°,∠CBH=45°,
∵∠COD=135°,
而∠AOB=90°,
∴∠1+∠2=45°,
∵∠OAB=∠2+∠3=45°,
∴∠1=∠3,
∴△OBC∽△DAO,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得BC=2
,解得BC=2![]() ,
,
∵△BCH为等腰直角三角形,
∴CH=BH=![]() BC=2,
BC=2,
∴C(-2,4),
把C(-2,4)代入y=![]() 得k=-2×4=-8.
得k=-2×4=-8.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目