题目内容
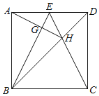
【题目】（综合与实践）如图①，在正方形ABCD中，点E、F分别在射线CD、BC上，且BF＝CE，将线段FA绕点F顺时针旋转90°得到线段FG，连接EG，试探究线段EG和BF的数量关系和位置关系．
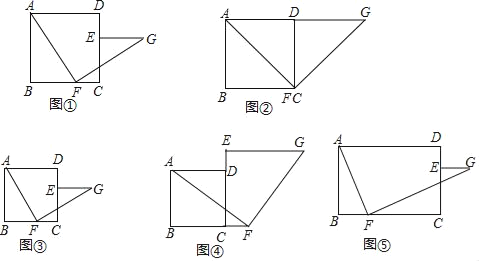
（观察与猜想）任务一：“智慧小组”首先考虑点E、F的特殊位置如图②，当点E与点D重合，点F与点C重合时，易知：EG与BF的数量关系是 ，EG与BF的位置关系是 ．
（探究与证明）任务二：“博学小组”同学认为E、F不一定必须在特殊位置，他们分两种情况，一种是点E、F分别在CD、BC边上任意位置时（如图③）；一种是点E、F在CD、BC边的延长线上的任意位置时（如图④），线段EG与BF的数量关系与位置关系仍然成立．请你选择其中一种情况给出证明．
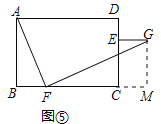
（拓展与延伸）“创新小组”同学认为，若将“正方形ABCD”改为“矩形ABCD，且
＝k（k≠1）”，点E、F分别在射线CD、BC上任意位置时，仍将线段FA绕点F顺时针旋转90°，并适当延长得到线段FG，连接EG（如图⑤），则当线段BF、CE、AF、FG满足一个条件 时，线段EG与BF的数量关系与位置关系仍然成立．（请你在横线上直接写出这个条件，无需证明）
【答案】【观察与猜想】EG＝BF，EG∥BF；【探究与证明】见解析;【拓展与延伸】
＝
＝k（k≠1）．
【解析】
【观察与猜想】先根据SAS证明△ABC≌△GDC，得出AB＝GD，∠GDC＝∠B＝90°，进而得出DG∥BC，△CDG是等腰直角三角形，再由等腰直角三角形的性质得出DG＝CD＝BC，即可得出结论；
【探究与证明】当点E、F分别在CD、BC边上任意位置时，作GM⊥BC，交BC延长线于M，先根据AAS证明△ABF≌△FMG，得出AB＝FM，BF＝MG，进而可得BF＝CM，而BF＝CE，可得MG＝CE，于是四边形CEGM是矩形，继而有EG＝CM，EG∥CM，即可得出结论；当点E、F在CD、BC边的延长线上的任意位置时，同上面的分析；
【拓展与延伸】作GM⊥BC，交BC延长线于M，先证明△ABF∽△FMG，得出
，结合已知可得出
，
，进而证出FM＝BC，GM＝CE，于是BF＝CM，然后证明四边形CEGM是矩形，进而得EG＝CM，EG∥CM，即可得出结论．
【观察与猜想】EG＝BF，EG∥BF；
证明：如图②，∵四边形ABCD是正方形，
∴∠B＝∠BCD＝∠ADC＝90°，AB＝BC＝CD＝AD，∠ACB＝∠ACD＝45°，
由旋转的性质得：GC＝AC，∠ACG＝90°，
∴∠ACB＝∠GCD＝45°，
∴△ABC≌△GDC（SAS），
∴AB＝GD，∠GDC＝∠B＝90°，
∴DG∥BC，△CDG是等腰直角三角形，
∴DG＝CD＝BC，
∵点E与点D重合，点F与点C重合，
∴EG＝BF，EG∥BF；
故答案为：EG＝BF，EG∥BF；
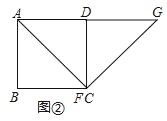
【探究与证明】证明：当点E、F分别在CD、BC边上任意位置时，如图③所示：
作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，
∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，
∴∠BAF+∠BFA＝90°，
由旋转的性质得：GF＝AF，∠AFG＝90°，
∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，
∴△ABF≌△FMG（AAS），
∴AB＝FM，BF＝MG，
∵AB＝BC，∴BF＝CM，
∵BF＝CE，∴MG＝CE，
∵MG∥CE，∴四边形CEGM是平行四边形，
又∵∠M＝90°，∴四边形CEGM是矩形，
∴EG＝CM，EG∥CM，
∴EG＝BF，EG∥BF；
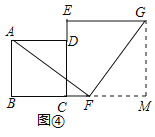
当点E、F在CD、BC边的延长线上的任意位置时，如图④所示：
作GM⊥BC，交BC延长线于M，则∠M＝90°，MG∥DC，
∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，
∴∠BAF+∠BFA＝90°，
由旋转的性质得：GF＝AF，∠AFG＝90°，
∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，
∴△ABF≌△FMG（AAS），
∴AB＝FM，BF＝MG，
∵AB＝BC，∴BF＝CM，
∵BF＝CE，∴MG＝CE，
∵MG∥CE，∴四边形CEGM是平行四边形，
又∵∠M＝90°，∴四边形CEGM是矩形，
∴EG＝CM，EG∥CM，
∴EG＝BF，EG∥BF；
【拓展与延伸】解：
＝k（k≠1）时，线段EG与BF的数量关系与位置关系仍然成立；理由如下：
作GM⊥BC，交BC延长线于M，如图⑤所示：则∠M＝90°，MG∥DC，
∵四边形ABCD是矩形，∴∠BCD＝∠B＝90°，
∴∠BAF+∠BFA＝90°，∠B＝∠M，
由旋转的性质得：∠AFG＝90°，∴∠BFA+∠MFG＝90°，
∴∠BAF＝∠MFG，∴△ABF∽△FMG，
∴，
∵＝k，∴＝k，＝k，
∴FM＝BC，GM＝CE，∴BF＝CM，
∵MG∥CE，∴四边形CEGM是平行四边形，
又∵∠M＝90°，∴四边形CEGM是矩形，
∴EG＝CM，EG∥CM，
∴EG＝BF，EG∥BF；
故答案为：＝k（k≠1）．
