ΧβΡΩΡΎ»ί
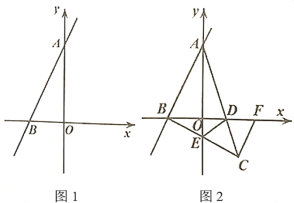
ΓΨΧβΡΩΓΩΫΪΝΫΩι–±±Ώ≥ΛœύΒ»ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«ΑεΑ¥»γΆΦΔΌΑΎΖ≈Θ§–±±ΏABΖ÷±πΫΜCDΘ§CE”ΎMΘ§NΒψΘ°
(1)»γΙϊΑ―ΆΦΔΌ÷–ΒΡΓςBCN»ΤΒψCΡφ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςACFΘ§Ν§Ϋ”FMΘ§»γΆΦΔΎΘ§«σ÷ΛΘΚΓςCMFΓ’ΓςCMNΘΜ
(2)ΫΪΓςCED»ΤΒψC–ΐΉΣΘ§‘ρΘΚ
ΔΌΒ±ΒψMΘ§N‘ΎAB…œ(≤Μ”κΒψAΘ§B÷ΊΚœ) ±Θ§œΏΕΈAMΘ§MNΘ§NB÷°Φδ”–“ΜΗω≤Μ±δΒΡΙΊœΒ ΫΘ§«κΡψ–¥≥ω’βΗωΙΊœΒ ΫΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΔΎΒ±ΒψM‘ΎAB…œΘ§ΒψN‘ΎABΒΡ―”≥ΛœΏ…œ(»γΆΦΔέ) ±Θ§ΔΌ÷–ΒΡΙΊœΒ Ϋ «Ζώ»‘»Μ≥…ΝΔΘΩ

ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈωΘΜ(2)ΔΌΦϊΫβΈωΘΜΔΎ»‘»Μ≥…ΝΔΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί–ΐΉΣΒΡ–‘÷ Ω…ΒΟCF=CNΘ§ΓœACF=ΓœBCNΘ§‘Ό«σ≥ωΓœACM+ΓœBCN=45ΓψΘ§¥”Εχ«σ≥ωΓœMCF=45ΓψΘ§»ΜΚσάϊ”ΟΓΑ±ΏΫ«±ΏΓ±÷ΛΟςΓςCMFΚΆΓςCMN»ΪΒ»Φ¥Ω…ΘΜ
Θ®2Θ©ΔΌΗυΨί»ΪΒ»»ΐΫ«–ΈΕ‘”Π±ΏœύΒ»Ω…ΒΟFM=MNΘ§‘ΌΗυΨί–ΐΉΣΒΡ–‘÷ Ω…ΒΟAF=BNΘ§ΓœCAF=ΓœB=45ΓψΘ§¥”Εχ«σ≥ωΓœBAF=90ΓψΘ§‘Όάϊ”ΟΙ¥Ι…Ε®άμΝ– ΫΦ¥Ω…ΒΟΫβΘΜ
ΔΎΑ―ΓςBCN»ΤΒψCΡφ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςACFΘ§ΗυΨί–ΐΉΣΒΡ–‘÷ Ω…ΒΟAF=BNCF=CNΘ§ΓœBCN=ΓœACFΘ§‘Ό«σ≥ωΓœMCF=ΓœMCNΘ§»ΜΚσάϊ”ΟΓΑ±ΏΫ«±ΏΓ±÷ΛΟςΓςCMFΚΆΓςCMN»ΪΒ»Θ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΕ‘”Π±ΏœύΒ»Ω…ΒΟMF=MNΘ§»ΜΚσάϊ”ΟΙ¥Ι…Ε®άμΝ– ΫΦ¥Ω…ΒΟΫβΘ°
Θ®1Θ©ΓΏΓςBCN»ΤΒψCΡφ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςACFΘ§
ΓύCF=CNΘ§ΓœACF=ΓœBCNΘ§
ΓΏΓœDCE=45ΓψΘ§
ΓύΓœACM+ΓœBCN=45ΓψΘ§
ΓύΓœACM+ΓœACF=45ΓψΘ§
Φ¥ΓœMCF=45ΓψΘ§
ΓύΓœMCF=ΓœMCNΘ§
‘ΎΓςCMFΚΆΓςCMN÷–Θ§
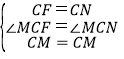 Θ§
Θ§
ΓύΓςCMFΓ’ΓςCMNΘ®SASΘ©ΘΜ
Θ®2Θ©ΔΌΓΏΓςCMFΓ’ΓςCMNΘ§
ΓύFM=MNΘ§
”÷ΓΏΓœCAF=ΓœB=45ΓψΘ§
ΓύΓœFAM=ΓœCAF+ΓœBAC=45Γψ+45Γψ=90ΓψΘ§
ΓύAM2+AF2=FM2Θ§
ΓύAM2+BN2=MN2ΘΜ
ΔΎ»γΆΦΘ§Α―ΓςBCN»ΤΒψCΡφ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςACFΘ§
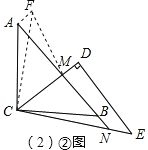
‘ρAF=BNΘ§CF=CNΘ§ΓœBCN=ΓœACFΘ§
ΓΏΓœMCF=ΓœACB-ΓœMCB-ΓœACF=90Γψ-Θ®45Γψ-ΓœBCNΘ©-ΓœACF=45Γψ+ΓœBCN-ΓœACF=45ΓψΘ§
ΓύΓœMCF=ΓœMCNΘ§
‘ΎΓςCMFΚΆΓςCMN÷–Θ§
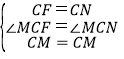 Θ§
Θ§
ΓύΓςCMFΓ’ΓςCMNΘ®SASΘ©Θ§
ΓύFM=MNΘ§
ΓΏΓœABC=45ΓψΘ§
ΓύΓœCAF=ΓœCBN=135ΓψΘ§
”÷ΓΏΓœBAC=45ΓψΘ§
ΓύΓœFAM=ΓœCAF-ΓœBAC=135Γψ-45Γψ=90ΓψΘ§
ΓύAM2+AF2=FM2Θ§
ΓύAM2+BN2=MN2Θ°

 «…―ß«…ΝΖœΒΝ–¥πΑΗ
«…―ß«…ΝΖœΒΝ–¥πΑΗ