Question

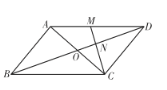
【题目】如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE、AH交于点G，则下列结论：①∠ABE＝∠DCE；②AG⊥BE；③S△BHE＝S△CHD；④∠AHB＝∠EHD．其中正确的是（　　）

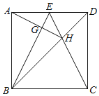
A.①③B.①②③④C.①②③D.①③④

Answer 1

【答案】B

【解析】

根据正方形的性质证得△BAE≌△CDE，推出∠ABE＝∠DCE，可知①正确；利用正方形性质证△ADH≌△CDH，求得∠HAD＝∠HCD，推出∠ABE＝∠HAD；求出∠ABE＋∠BAG＝90°；最后在△AGE中根据三角形的内角和是180°求得∠AGE＝90°即可得到②正确．根据AD∥BC，求出S△BDE＝S△CDE，推出S△BDES△DEH＝S△CDES△DEH，即：S△BHE＝S△CHD，故③正确；由∠AHD＝∠CHD，得到邻补角和对顶角相等得到∠AHB＝∠EHD，故④正确；

解：∵四边形ABCD是正方形，E是AD边上的中点，

∴AE＝DE，AB＝CD，∠BAD＝∠CDA＝90°，

∴△BAE≌△CDE（SAS），

∴∠ABE＝∠DCE，

故①正确；

∵四边形ABCD是正方形，

∴AD＝DC，∠ADB＝∠CDB＝45°，DH＝DH，

∴△ADH≌△CDH（SAS），

∴∠HAD＝∠HCD，

∵∠ABE＝∠DCE

∴∠ABE＝∠HAD，

∵∠BAD＝∠BAH＋∠DAH＝90°，

∴∠ABE＋∠BAH＝90°，

∴∠AGB＝180°90°＝90°，

∴AG⊥BE，

故②正确；

∵AD∥BC，

∴S△BDE＝S△CDE，

∴S△BDES△DEH＝S△CDES△DEH，

即：S△BHE＝S△CHD，

故③正确；

∵△ADH≌△CDH，

∴∠AHD＝∠CHD，

∴∠AHB＝∠CHB，

∵∠BHC＝∠DHE，

∴∠AHB＝∠EHD，

故④正确；

故选：B．