题目内容
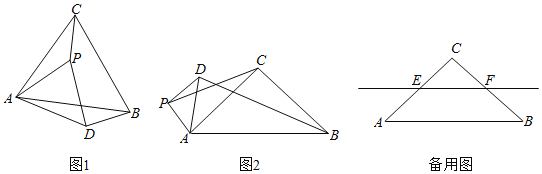
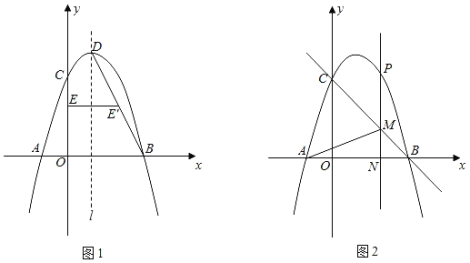
【题目】如图1，二次函数y＝﹣x2+bx+c的图象与x轴交于A(﹣1，0)，B(3，0)两点，与y轴交于点C，直线l是抛物线的对称轴，D是抛物线的顶点．
（1）求该抛物线的函数表达式；
（2）如图1，连结BD，线段OC上点E关于直线l的对称点E'恰好在线段BD上，求点E的坐标；
（3）如图2，点P是直线BC上方抛物线上一动点，过点P作y轴的平行线分别与BC交于点M，与x轴交于点N．试问：抛物线上是否存在点Q，使得△PQN与△AMN的面积相等，且线段PQ的长度最小？如果存在，请直接写出点Q的坐标；如果不存在，请说明理由．
【答案】（1）y＝﹣x2+2x+3；（2）E(0，2)；（3）存在，点Q(
，
)或(
，)
【解析】
（1）先根据抛物线的解析式判断出二次项的系数为﹣1，再根据点A，B坐标的特点按交点式设出化简即可得出结论；
（2）先确定出直线BD的解析式，设出点E的坐标，进而得出点E'的坐标，代入直线BD解析式求解，即可得出结论；
（3）设出点P的坐标，表示出点M，N的坐标，再设出点Q到直线PM的距离为h，根据△PQN与△AMN的面积相等，求出h＝1，进而得出点Q的坐标，再分两种情况，利用PQ最短，求出m，即可得出结论．
解：（1）∵二次函数y＝﹣x2+bx+c的图象与x轴交于A（﹣1，0），B（3，0），
∴抛物线的解析式为y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3；
（2）由（1）知，抛物线的解析式为y＝﹣x2+2x+3＝﹣（x﹣1）2+4，
∴D（1，4），
∵B（3，0），
∴直线BD的解析式为y＝﹣2x+6，
设点E（0，a），
∵点E'是点E关于抛物线对称轴对称的点，
∴E'（2，a），
∵点E'（2，a）在直线BD上，
∴﹣2×2+6＝a，
∴a＝2，
∴E（0，2）；
（3）由（1）知，抛物线的解析式为y＝﹣x2+2x+3，
∴C（0，3），
∵B（3，0），
∴直线BC的解析式为y＝﹣x+3，
设点P（m，﹣m2+2m+3），
∴M（m，﹣m+3），N（m，0），
∴S△AMN＝ANMN＝（m+1）（﹣m+3）＝﹣（m+1）（m﹣3），
设点Q到直线PM的距离为h，
∴S△PQN＝PNh＝（﹣m2+2m+3）h，
∵△PQN与△AMN的面积相等，
∴﹣（m+1）（m﹣3）h＝﹣（m+1）（m﹣3），
∴h＝1
∴Q的横坐标为（m+1）或（m﹣1），
∴Q（m+1，﹣m2+4）或（m﹣1，﹣m2+4m），
当Q（m+1，﹣m2+4）时，PQ2＝（m+1﹣m）2+[﹣m2+4﹣（﹣m2+2m+3）]2＝（2m﹣1）2+1，
当m＝时，PQ2最小，即PQ最小，此时Q（，），
当Q（m﹣1，﹣m2+4m）时，PQ2＝（m﹣1﹣m）2+[﹣m2+4m﹣（﹣m2+2m+3）]2＝（2m﹣3）2+1，
当m＝时，PQ2最小，即PQ最小，此时Q（，），
即满足条件的点Q（，）或（，）．
