题目内容
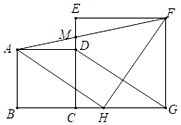
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ、DP交于点O,并分别与边CD、BC交于点F、E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD<S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的是_____.(请将正确结论的序号填写在横线上)
,其中正确结论的是_____.(请将正确结论的序号填写在横线上)

【答案】①④
【解析】
由四边形ABCD是正方形可得 AD=BC、∠DAB=∠ABC=90°,再根据全等三角形的性质可得∠P=∠Q,最后根据余角的性质可得AQ⊥DP;故①正确;根据相似三角形的性质可得AO2=ODOP,由OD≠OE,得到OA2≠OEOP;故②错误;根据全等三角形的性质得到CF=BE,DF=CE,则S△ADF﹣S△DFO=S△DCE﹣S△DOF,即S△AOD=S四边形OECF;故③错误;根据相似三角形的性质可得BE=![]() ,求得QE=
,求得QE=![]() ,QO=
,QO=![]() ,OE=
,OE=![]() ,最后由三角函数的定义即可得到结论.
,最后由三角函数的定义即可得到结论.
解:①∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,
∵BP=CQ,
∴AP=BQ,
在△DAP与△ABQ中,
 ,
,
∴△DAP≌△ABQ(SAS),
∴∠P=∠Q,
∵∠Q+∠QAB=90°,
∴∠P+∠QAB=90°,
∴∠AOP=90°,
∴AQ⊥DP,故①正确;
②∵∠DOA=∠AOP=90°,∠ADO+∠P=∠ADO+∠DAO=90°,
∴∠DAO=∠P,
∴△DAO∽△APO,
∴![]() ,
,
∴AO2=ODOP,
∵AE>AB,
∴AE>AD,
∴OD≠OE,
∴OA2≠OEOP;故②错误;
③在△CQF与△BPE中
 ,
,
∴△CQF≌△BPE(ASA),
∴CF=BE,
∴DF=CE,
在△ADF与△DCE中,
 ,
,
∴△ADF≌△DCE(SAS),
∴S△ADF﹣S△DFO=S△DCE﹣S△DOF,
即S△AOD=S四边形OECF;故③错误;
④∵BP=1,AB=3,
∴AP=4,
∵△PBE∽△PAD,
∴![]() ,
,
∴BE=![]() ,
,
∴QE=![]() ,
,
∵△QOE∽△PAD,
∴![]() =
=![]() ,
,
∴QO=![]() ,OE=
,OE=![]() ,
,
∴AO=5﹣QO=![]() ,
,
∴tan∠OAE=![]() ,故④正确,
,故④正确,
故答案为:①④.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案【题目】某超市一段时期内对某种商品经销情况进行统计得到该商品的销售数量![]() (件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价
(件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价![]() (元/件,
(元/件,![]() )成反比例,销售过程中得到的部分数据如下:
)成反比例,销售过程中得到的部分数据如下:
售价 | 8 | 10 |
销售数量 | 70 | 58 |
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当该商品销售数量为50件时,求每件商品的售价;
(3)设销售总额为![]() ,求
,求![]() 的最大值.
的最大值.