Question

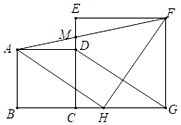
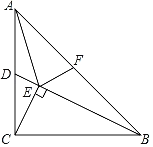
【题目】如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，D是边AC的中点，CE⊥BD于E．若F是边AB上的点，且使△AEF为等腰三角形，则AF的长为_____．

Answer 1

【答案】或或

【解析】

由相似三角形的性质可求AH的长，BH的长，分三种情况讨论，由等腰三角形的性质和勾股定理可求解．

解：∵∠ACB＝90°，AC＝BC＝2，

∴AB＝

∵∠DCB＝90°，CE⊥BD，

∴△CDE∽△BDC，

∴CD2＝DEDB，

∵AD＝CD，

∴AD2＝DEDB，

∴，

∵∠ADE∠ADB，

△DAE∽△DBA；

∴，

∴AE＝，

∵DE＝，BD＝，

∴BE＝，

如图1中，若AE＝AF时，

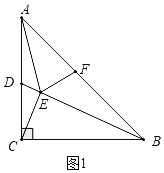
∴AF＝；

如图2中，若FE＝AE时，过点E作EJ⊥AB于J，

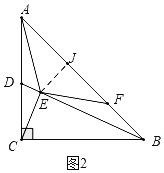
∵JE2＝AE2﹣AJ2＝EB2﹣BJ2，

∴﹣AJ2＝﹣（2﹣AJ）2，

∴AJ＝，

∵AE＝EF，EJ⊥AF，

∴AF＝2AJ＝，

如图3中，若EF＝AF时，过点E作EJ⊥AB于J，

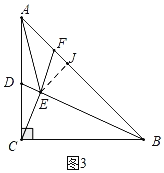
∵EJ2＝AE2﹣AJ2＝EF2﹣FJ2，

∴﹣＝AF2﹣（﹣AF）2，

∴AF＝，

综上所述：AD的长为或或．

故答案为：或或．