题目内容
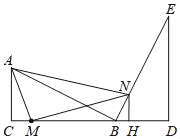
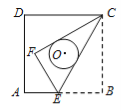
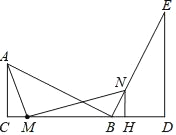
【题目】两个含30°角的直角三角形ABC和直角三角形BED如图那样拼接,C、B、D在同一直线上,AC=BD,∠ABC=∠E=30°,∠ACB=∠BDE=90°,M为线段CB上一个动点(不与C、B重合).过M作MN⊥AM,交直线BE于N,过N作NH⊥BD于H.
(1)当M在什么位置时,△AMC∽△NBH?
(2)设AC=![]() .
.
①若CM=2,求BH的长;
②当M沿线段CB运动时,连接AN(图中未连),求△AMN面积的取值范围.
【答案】(1)见解析;(2)①BH=2;②![]()
【解析】
(1)先确定△AMC和△NBH都是直角三角形,再根据垂直平行可得:∠BNH=30°,由相似三角形的对应关系,可得:当∠CAM=30°时,可得:△AMC∽△NBH,从而确定M的位置;
(2)①设BH=x,则HN=![]() ,MH=1+x,证明△ACM∽△MHN,则
,MH=1+x,证明△ACM∽△MHN,则![]() ,即
,即![]() ,可得BH的长;
,可得BH的长;
②由题得AC=BD=![]() ,BC=ED=3,∠NBH=60°,设CM=x(0<x<3),BH=t,则HN=
,BC=ED=3,∠NBH=60°,设CM=x(0<x<3),BH=t,则HN=![]() t,MB=3﹣x,从而MH=3﹣x+t,同理△ACM∽△MHN得列方程可得:BH=x,分别表示AM和MN的长,利用三角形面积公式可得S△AMN=
t,MB=3﹣x,从而MH=3﹣x+t,同理△ACM∽△MHN得列方程可得:BH=x,分别表示AM和MN的长,利用三角形面积公式可得S△AMN=![]() =
=![]() ,由x的取值范围可得结论.
,由x的取值范围可得结论.
解:(1)由题知,NH⊥BD,ED⊥BD,
∴∠BNH=30°,又△AMC与△NBH都是直角三角形,
∴当∠CAM=30°,即当M位于∠CAB的平分线上时,△AMC∽△NBH;
(2)①Rt△ACB中,∵AC=![]() ,CM=2,∠CAB=60°,
,CM=2,∠CAB=60°,
∴CB=3,MB=1,
设BH=x,
∵∠EBD=60°,
∴HN=![]() x,MH=1+x,
x,MH=1+x,
∵MN⊥AM,
∴∠AMC+∠NMH=90°,又∠AMC+∠CAM=90°,
∴∠CAM=∠HMN,
∵∠ACM=∠MHN=90°,
∴△ACM∽△MHN
∴![]() ,即
,即![]() ,x=2,即BH=2
,x=2,即BH=2
②由题得AC=BD=![]() ,BC=ED=3,∠NBH=60°,
,BC=ED=3,∠NBH=60°,
∴tan30°=![]() =
=![]() ,
,
设CM=x(0<x<3),BH=t,则HN=![]() t,MB=3﹣x,
t,MB=3﹣x,
从而MH=3﹣x+t,
由△ACM∽△MHN得![]() ,
,
(3﹣x)(t﹣x)=0,x<3,
∴t=x,即有BH=x,
MH=MB+BH=3﹣x+x=3,
AM=![]() ,MN=
,MN=![]() ,
,
S△AMN=![]()
=![]() ,
,
∴![]()