题目内容
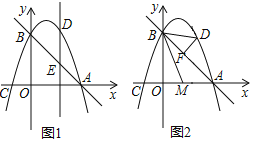
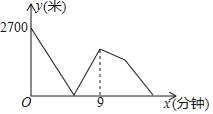
【题目】A,B两地之间有一条直线跑道,甲,乙两人分别从A,B同时出发,相向而行匀速跑步,且乙的速度是甲速度的80%,当甲,乙分别到达B地,A地后立即调头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行),甲,乙两人之间的距离y(米)与跑步时间x(分钟)之间的关系如图所示,则他们在第二次相遇时距B地_____米.
【答案】1687.5
【解析】
观察函数图象,可知甲用9分钟到达B地,由速度=路程÷时间可求出甲的速度,结合甲、乙速度间的关系可求出乙的初始速度及乙加速后的速度,利用时间=路程÷速度可求出乙到达A地时的时间,设两人第二次相遇的时间为t分钟,由二者第二次相遇走过的总路程为A,B两点间距离的3倍,即可得出关于t的一元一次方程,解之即可得出t值,再利用甲、乙二人在第二次相遇时距B地的距离=甲的总路程﹣2700,即可求出结论.
解:甲的速度为2700÷9=300(米/分钟),
乙的初始速度为300×80%=240(米/分钟),
乙到达A地时的时间为2700÷240=![]() (分钟),
(分钟),
乙加速后的速度为240×(1+25%)=300(米/分钟).
设两人第二次相遇的时间为t分钟,
根据题意得:300t+2700+300(t﹣![]() )=2700×3,
)=2700×3,
解得:t=![]() ,
,
∴他们在第二次相遇时距B地300t﹣2700=1687.5.
故答案为:1687.5.

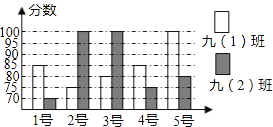
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.