题目内容
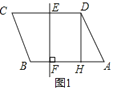
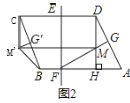
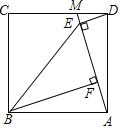
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
【答案】(1)证明见解析;(2)sin∠EBF=![]() .
.
【解析】(1)通过证明△ABF≌△DAE得到BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,利用四边形ABED的面积等于△ABE的面积与△ADE的面积之和得到![]() xx+
xx+![]() x2=24,解方程求出x得到AE=BF=6,则EF=x﹣2=4,然后利用勾股定理计算出BE,最后利用正弦的定义求解.
x2=24,解方程求出x得到AE=BF=6,则EF=x﹣2=4,然后利用勾股定理计算出BE,最后利用正弦的定义求解.
(1)证明:∵四边形ABCD为正方形,
∴BA=AD,∠BAD=90°,
∵DE⊥AM于点E,BF⊥AM于点F,
∴∠AFB=90°,∠DEA=90°,
∵∠ABF+∠BAF=90°,∠EAD+∠BAF=90°,
∴∠ABF=∠EAD,
在△ABF和△DAE中,
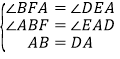 ,
,
∴△ABF≌△DAE(AAS),
∴BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,
∵四边形ABED的面积为24,
∴![]() xx+
xx+![]() x2=24,解得x1=6,x2=﹣8(舍去),
x2=24,解得x1=6,x2=﹣8(舍去),
∴EF=x﹣2=4,
在Rt△BEF中,BE=![]() =2
=2![]() ,
,
∴sin∠EBF=![]() .
.

练习册系列答案
相关题目