题目内容
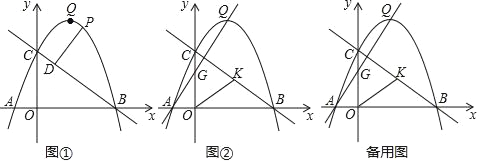
【题目】已知二次函数![]() 的图像与x轴交于点(-2,0)、(
的图像与x轴交于点(-2,0)、(![]() ),且
),且![]() ,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
根据已知画出图象,根据对称轴和开口方向可判断①;把x=-2代入得:4a-2b+c=0,可判断②;由②的结论,可得 2a-b=![]() ,根据c的取值范围可得2a-b的取值范围,可判断③;根据图象与x轴的交点可用x2表示对称轴,易确定a,b的取值范围,可判断④.
,根据c的取值范围可得2a-b的取值范围,可判断③;根据图象与x轴的交点可用x2表示对称轴,易确定a,b的取值范围,可判断④.
解:画出图象如图,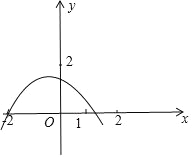
∵开口向下,
∴a<0,
∵x=![]() <0,
<0,
∴b<0,
∴ab>0,
∴①正确;
根据二次函数y=ax2+bx+c的图象与x轴交于点(2,0)、(x2,0),且1<x2<2,与y轴的正半轴的交点在(0,2)的下方,把x=2代入得:4a2b+c=0,
∴②正确;
由4a2b+c=0得2ab=![]() ,
,
而0<c<2,
∴1<![]() <0
<0
∴1<2ab<0
∴2ab+1>0,
∴③错误;
∵图象与x轴两交点为(2,0),(x2,0),且1<x2<2,
对称轴x=![]() =
=![]() ,
,
则对称轴![]() <
<![]() <0,且a<0,
<0,且a<0,
∴a>b
∴a<b<0,
由抛物线与y轴的正半轴的交点在(0,2)的下方,得c>0,
即a<b<c,
∴④正确;
所以正确的选项为①②④。
故选:C

【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.