题目内容
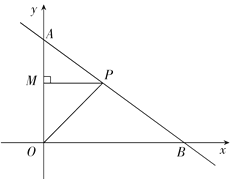
【题目】如图:一次函数![]() 的图象与坐标轴交于A、B两点,点P是函数
的图象与坐标轴交于A、B两点,点P是函数![]() (0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.
(0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.
(1)当AP为何值时,△OPM的面积最大?并求出最大值;
(2)当△BOP为等腰三角形时,试确定点P的坐标.
【答案】(1)AP=![]() ;(2)点P的坐标为(
;(2)点P的坐标为(![]() ,
,![]() )或(2,
)或(2,![]() ).
).
【解析】
(1)令P点坐标为(x0,y0),根据三角形面积公式列出S△OPM关于x0的二次函数解析式,确定最大值,进而根据相似比求出当△OPM面积最大时AP的长即可;(2)将情况分为BO=BP以及OP=BP两种进行讨论:①当BO=BP时,根据三角形相似求出MP的长,即P点的横坐标,将P点横坐标代入一次函数解析式,即可得到P点的坐标;②当OP=BP时,如图,过点P作PM⊥OB于点N,根据等腰三角形的性质得到ON=![]() OB,ON的长即为P点的横坐标,将ON=2代入一次函数解析式中即可求出P点的纵坐标.
OB,ON的长即为P点的横坐标,将ON=2代入一次函数解析式中即可求出P点的纵坐标.
(1)令点![]() 的坐标为
的坐标为![]() ,
,![]()
![]() 轴,
轴,![]()
将![]() 代入得
代入得![]()
![]() 当
当![]() 时,
时,![]() 的面积,有最大值
的面积,有最大值![]() ,
,
即:![]() ,
,
![]() ,
,
![]()
![]()
即![]()
![]() 直线
直线![]() 分别交两坐标轴于点
分别交两坐标轴于点![]() 、
、![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
(2)①在![]() 中,当
中,当![]() 时
时
![]() ,
,![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
将![]() 代入代入
代入代入![]() 中,得
中,得![]()
![]() ,
,![]() ;
;
②在![]() 中,当
中,当![]() 时,如图,
时,如图,
过点![]() 作
作![]() 于点
于点![]()
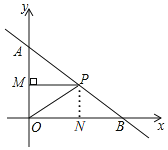
![]() ,
,
![]()
将![]() 代入
代入![]() 中得,
中得,![]()
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
即:点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() .
.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目