题目内容

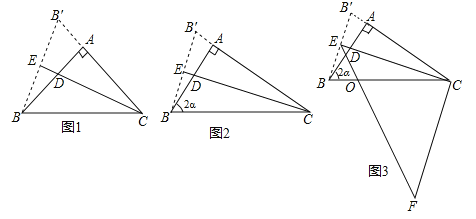
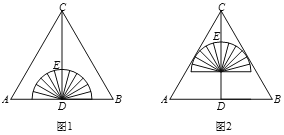
【题目】如图1，将一个量角器与一张等边三角形(△ABC)纸片放置成轴对称图形，CD⊥AB,垂足为D，半圆(量角器)的圆心与点D重合，此时，测得顶点C到量角器最高点的距离CE＝2cm，将量角器沿DC方向平移1cm，半圆(量角器)恰与△ABC的边AC，BC相切，如图2,则AB的长为__________cm.

【答案】

【解析】

如图，设图（2）中半圆的圆心为O，与BC的切点为M，连接OM，根据切线的性质可以得到∠OMC＝90°，而根据已知条件可以得到∠DCB＝30°，设AB为2xcm，根据等边三角形得到CDxcm，而CE＝2cm，又将量角器沿DC方向平移1cm，由此得到半圆的半径为OM=（x﹣2）cm，OC＝（x﹣1）cm，然后在Rt△OCM中利用三角函数可以列出关于x的方程，解方程即可求解．

如图，设图（2）中半圆的圆心为O，与BC的切点为M，连接OM，则OM⊥MC，∴∠OMC＝90°，依题意得：∠DCB＝30°，设AB为2xcm．

∵△ABC是等边三角形，∴CDxcm，而CE＝2cm，又将量角器沿DC方向平移1cm，∴半圆的半径为OM=（x﹣2）cm，OC＝（x﹣1）cm，∴sin∠DCB，∴，∴x，∴AB＝2x＝2（cm）．

故答案为：2．

练习册系列答案
相关题目

【题目】如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.

（1）求证：△BDE≌△BCE；

（2）试判断四边形ABED的形状，并说明理由．

【题目】已知在Rt△ABC中，∠BAC＝90°，CD为∠ACB的平分线，将∠ACB沿CD所在的直线对折，使点B落在点B′处，连结AB'，BB'，延长CD交BB'于点E，设∠ABC＝2α（0°＜α＜45°）．

（1）如图1，若AB＝AC，求证：CD＝2BE；

（2）如图2，若AB≠AC，试求CD与BE的数量关系（用含α的式子表示）；

（3）如图3，将（2）中的线段BC绕点C逆时针旋转角（α+45°），得到线段FC，连结EF交BC于点O，设△COE的面积为S1，△COF的面积为S2，求（用含α的式子表示）．

【题目】如图，在△ABC中，∠ACB=90°，AB=9，cosB=，把△ABC绕着点C旋转，使点B与AB边上的点D重合，点A落在点E，则点A、E之间的距离为 ．

【题目】如图，Rt△ABC中，∠C=90°，BC=8cm，AC=6cm．点P从B出发沿BA 向A运动，速度为每秒1cm，点E是点B以P为对称中心的对称点．点P运动的同时，点Q从A出发沿AC向C运动，速度为每秒2cm ．当点Q到达顶点C时，P，Q同时停止运动．设P， Q两点运动时间为t秒．

（1）当t为何值时，PQ∥BC ？

（2）设四边形PQCB的面积为y，求y关于t的函数解析式;

（3）四边形PQCB的面积与△APQ面积比能为3：2吗？若能，求出此时t的值；若不能，请说明理由；

（4）当t为何值时，△AEQ为等腰三角形？

【题目】如图，AB，AC是⊙O的两条切线，B，C为切点，连接CO并延长交AB于点D，交⊙O于点E，连接BE，连接AO．

（1）求证：AO∥BE；

（2）若DE＝2，tan∠BEO＝，求DO的长．

【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

（1）求证：AF=DC；

（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

【题目】如图：一次函数 的图象与坐标轴交于A、B两点，点P是函数（0＜x＜4）图象上任意一点，过点P作PM⊥y轴于点M，连接OP.

（1）当AP为何值时，△OPM的面积最大？并求出最大值；

（2）当△BOP为等腰三角形时，试确定点P的坐标.

【题目】如图，AB，AC是⊙O的两条切线，B，C为切点，连接CO并延长交AB于点D，交⊙O于点E，连接BE，连接AO．

（1）求证：AO∥BE；

（2）若DE＝2，tan∠BEO＝，求DO的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网