ƒøƒĞ»ı
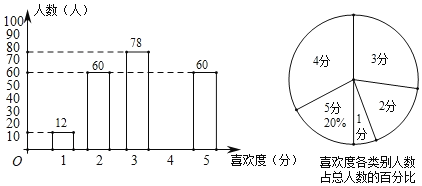
°æƒø°ø√‡—Ùƒ≥π´Àæœ˙ ğÕ≥º∆¡À√ø∏ˆœ˙ 𑱑Ѓ≥‘¬µƒœ˙ ğ∂Ó£¨ªÊ÷∆¡À»Áœ¬’ğœşÕ≥º∆Õº∫Õ…»–ŒÕ≥º∆Õº£∫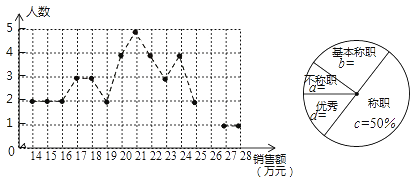
…Ëœ˙ 𑱵ƒ‘¬œ˙ ğ∂ÓŒ™x£®µ•Œª£∫ÕÚ‘™£©°£œ˙ ğ≤øπÊ∂®£∫µ±x<16 ±£¨Œ™°∞≤ª≥∆÷∞°±£¨µ± ![]() ±Œ™°∞ª˘±æ≥∆÷∞°±£¨µ±
±Œ™°∞ª˘±æ≥∆÷∞°±£¨µ±![]() ±Œ™°∞≥∆÷∞°±£¨µ±
±Œ™°∞≥∆÷∞°±£¨µ±![]() ±Œ™°∞”≈–„°±.∏˘æı“‘…œ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
±Œ™°∞”≈–„°±.∏˘æı“‘…œ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©≤π»´’ğœşÕ≥º∆Õº∫Õ…»–ŒÕ≥º∆Õº£ª
£®2£©«ÛÀ˘”–°∞≥∆÷∞°±∫Õ°∞”≈–„°±µƒœ˙ 𑱜˙ ğ∂Óµƒ÷–Œª ˝∫Õ÷Ğ ˝£ª
£®3£©Œ™¡Àµ˜∂Øœ˙ 𑱵ƒª˝º´–‘£¨œ˙ ğ≤øæˆ∂®÷∆∂®“ª∏ˆ‘¬œ˙ ğ∂ÓΩ±¿¯±Í◊º£¨∑≤‘¬œ˙ ğ∂Ó¥ÔµΩªÚ≥¨π˝’‚∏ˆ±Í◊ºµƒœ˙ ğ‘±Ω´ªÒµ√Ω±¿¯°£»Áπ˚“™ πµ√À˘”–°∞≥∆÷∞°±∫Õ°∞”≈–„°±µƒœ˙ 𑱵ƒ“ª∞λÀ‘±ƒİªÒΩ±£¨‘¬œ˙ ğ∂ÓΩ±¿¯±Í◊º”¶∂®Œ™∂‡…ŸÕÚ‘™£®Ω·π˚»•’˚ ˝£©£ø≤¢ºÚ ˆ∆‰¿Ì”….
°æ¥∞∏°ø£®1£©≤π»´Õ≥º∆Õº»ÁÕºº˚Ω‚Œˆ£ª£®2£© °∞≥∆÷∞°±µƒœ˙ 𑱑¬œ˙ ğ∂Óµƒ÷–Œª ˝Œ™£∫22ÕÚ£¨÷Ğ ˝£∫21ÕÚ£ª°∞”≈–„°±µƒœ˙ 𑱑¬œ˙ ğ∂Óµƒ÷–Œª ˝Œ™£∫26ÕÚ£¨÷Ğ ˝£∫25ÕÚ∫Õ26ÕÚ£ª£®3£©‘¬œ˙ ğ∂ÓΩ±¿¯±Í◊º”¶∂®Œ™22ÕÚ‘™.
°æΩ‚Œˆ°ø
£®1£© ∏˘æı≥∆÷∞µƒ»À ˝º∞∆‰À˘’º∞Ÿ∑÷±»«Ûµ√◊İ»À ˝£¨ æı¥À«Ûµ√≤ª≥∆÷∞°¢ ª˘±æ≥∆÷∞∫Õ”≈–„µƒ∞Ÿ∑÷±»£¨ ‘Ÿ«Û≥ˆ”≈–„µƒ◊İ»À ˝£¨ ¥”∂¯µ√≥ˆœ˙ ğ 26 ÕÚ‘™µƒ»À ˝£¨ æı¥Àº¥ø…≤π»´Õº–Œ £Æ
£®2£© ∏˘æı÷–Œª ˝∫Õ÷Ğ ˝µƒ∂®“«ÛΩ‚ø…µ√£ª
£®3£© ∏˘æı÷–Œª ˝µƒ“‚“«۵√≥∆÷∞∫Õ”≈–„µƒ÷–Œª ˝º¥ø…µ√≥ˆ∑˚∫œ“™«Ûµƒ ˝æı £Æ
£®1£©“¿Ã‚ø…µ√£∫
°∞≤ª≥∆÷∞°±»À ˝Œ™£∫2+2=4£®»À£©£¨
°∞ª˘±æ≥∆÷∞°±»À ˝Œ™£∫2+3+3+2=10£®»À£©£¨
°∞≥∆÷∞°±»À ˝Œ™£∫4+5+4+3+4=20£®»À£©£¨
°‡◊İ»À ˝Œ™£∫20°¬50%=40£®»À£©£¨
°‡≤ª≥∆÷∞°±∞Ÿ∑÷±»£∫a=4°¬40=10%£¨
°∞ª˘±æ≥∆÷∞°±∞Ÿ∑÷±»£∫b=10°¬40=25%£¨
°∞”≈–„°±∞Ÿ∑÷±»£∫d=1-10%-25%-50%=15%£¨
°‡°∞”≈–„°±»À ˝Œ™£∫40°¡15%=6£®»À£©£¨
°‡µ√26∑÷µƒ»À ˝Œ™£∫6-2-1-1=2£®»À£©£¨
≤π»´Õ≥º∆Õº»ÁÕºÀ˘ æ£∫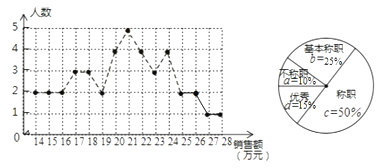
£®2£©”…’ğœşÕ≥º∆Õºø…÷™£∫°∞≥∆÷∞°±20ÕÚ4»À£¨21ÕÚ5»À£¨22ÕÚ4»À£¨23ÕÚ3»À£¨24ÕÚ4»À£¨
°∞”≈–„°±25ÕÚ2»À£¨26ÕÚ2»À£¨27ÕÚ1»À£¨28ÕÚ1»À£ª
°∞≥∆÷∞°±µƒœ˙ 𑱑¬œ˙ ğ∂Óµƒ÷–Œª ˝Œ™£∫22ÕÚ£¨÷Ğ ˝£∫21ÕÚ£ª
°∞”≈–„°±µƒœ˙ 𑱑¬œ˙ ğ∂Óµƒ÷–Œª ˝Œ™£∫26ÕÚ£¨÷Ğ ˝£∫25ÕÚ∫Õ26ÕÚ£ª
£®3£©”…£®2£©÷™‘¬œ˙ ğ∂ÓΩ±¿¯±Í◊º”¶∂®Œ™22ÕÚ.
°ş°∞≥∆÷∞°±∫Õ°∞”≈–„°±µƒœ˙ 𑱑¬œ˙ ğ∂Óµƒ÷–Œª ˝Œ™£∫22ÕÚ£¨
°‡“™ πµ√À˘”–°∞≥∆÷∞°±∫Õ°∞”≈–„°±µƒœ˙ 𑱵ƒ“ª∞λÀ‘±ƒİªÒΩ±£¨‘¬œ˙ ğ∂ÓΩ±¿¯±Í◊º”¶∂®Œ™22ÕÚ‘™.

 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏°æƒø°øƒ≥”Œ”æπı√øƒÍœƒºæÕ∆≥ˆ¡Ω÷÷”Œ”æ∏∂∑—∑Ω Ω£¨∑Ω Ω“ª£∫œ»π∫¬Úª·‘±÷§£¨√ø’≈ª·‘±÷§100‘™£¨÷ªœŞ±æ»Àµ±ƒÍ π”√£¨∆æ÷§”Œ”æ√ø¥Œ‘Ÿ∏∂∑—5‘™£ª∑Ω Ω∂˛£∫≤ªπ∫¬Úª·‘±÷§£¨√ø¥Œ”Œ”æ∏∂∑—9‘™£Æ
…Ë–°√˜º∆ªÆΩ҃͜ƒºæ”Œ”楌 ˝Œ™x£®xŒ™’˝’˚ ˝£©£Æ
£®I£©∏˘æı“‚£¨ÃÓ–¥œ¬±Ì£∫
”Œ”楌 ˝ | 10 | 15 | 20 | °≠ | x |
∑Ω Ω“ªµƒ◊İ∑—”√£®‘™£© | 150 | 175 | ______ | °≠ | ______ |
∑Ω Ω∂˛µƒ◊İ∑—”√£®‘™£© | 90 | 135 | ______ | °≠ | ______ |
£®¢Ú£©»Ù–°√˜º∆ªÆΩ҃͜ƒºæ”Œ”浃◊İ∑—”√Œ™270‘™£¨—°‘Òƒƒ÷÷∏∂∑—∑Ω Ω£¨À˚”Œ”浃¥Œ ˝±»Ωœ∂‡£ø
£®¢Û£©µ±x>20 ±£¨–°√˜—°‘Òƒƒ÷÷∏∂∑—∑Ω Ω∏¸∫œÀ„£ø≤¢Àµ√˜¿Ì”…£Æ
°æƒø°øŒ™¡À≤Œº”°∞æ£÷ı –÷––°—ß…˙ ◊ΩÏ ´¥ ¥Ûª·°±£¨ƒ≥–£∞ÀƒÍº∂µƒ¡Ω∞‡—ß…˙Ω¯––¡À‘§—°£¨∆‰÷–∞‡…œ«∞5√˚—ß…˙µƒ≥…º®£®∞Ÿ∑÷÷∆£©∑÷±Œ™£∫∞À£®1£©∞‡86£¨85£¨77£¨92£¨85£ª∞À£®2£©∞‡79£¨85£¨92£¨85£¨89£ÆÕ®π˝ ˝æı∑÷Œˆ£¨¡–±Ì»Áœ¬£∫
∞‡º∂ | ∆Ωæ˘∑÷ | ÷–Œª ˝ | ÷Ğ ˝ | ∑Ω≤Ó |
∞À£®1£© | 85 | b | c | 22.8 |
∞À£®2£© | a | 85 | 85 | 19.2 |
£®1£©÷±Ω”–¥≥ˆ±Ì÷–a£¨b£¨cµƒ÷µ£ª
£®2£©∏˘æı“‘…œ ˝æı∑÷Œˆ£¨ƒ„»œŒ™ƒƒ∏ˆ∞‡«∞5√˚Õ¨—ßµƒ≥…º®Ωœ∫√£øÀµ√˜¿Ì”…£Æ