��Ŀ����
����Ŀ����ͼ����֪A��2��0����B��1��m2��4m+5����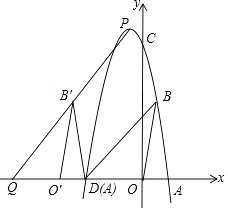
��1��ֱ���жϡ�ABO��ʲôͼ�Σ�
��2�����S��ABO����Сֵ����m��ֵ��
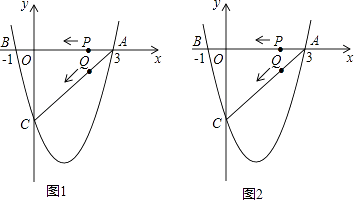
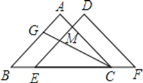
��3��������y=����x��2����x��n��������B����y�ύ�ڵ�C����x�ύ������A��D��
���ú�m��ʽ�ӱ�ʾ��C�͵�D���ꣻ
�ڵ�P����������x���Ϸ���һ�㣬PQ��BD��x���ڵ�Q������ABO����ƽ�Ƶ���A��B��O�䣬��A��B��O�Ķ�Ӧ��ֱ���A�䣬B�䣬O�䣬����A'���D�غ�ʱ����B'���߶�PQ�ϣ������Pǡ���������߶��㣬��m��ֵ��
���𰸡�
��1��
�⣺��A��2��0����B��1��m2��4m+5����
���B���߶�OA�Ĵ�ֱƽ�����ϣ�
��OB=AB��
���ABO �ǵ���������
��2��
�⣺��S��ABO= ![]() ��2����m2��4m+5��=m2��4m+5=��m��2��2+1��
��2����m2��4m+5��=m2��4m+5=��m��2��2+1��
�൱m=2ʱ��S��ABO ����Сֵ
��3��
�⣺�ٰ�B��1��m2��4m+5������
y=����x��2����x��n����m2��4m+5=����1��2����1��n����
��n=����m��2��2��
��y=��x2+����m2+4m��2��x+2��m��2��2��
��x=0����y=2��m��2��2��
��C��0��2��m��2��2����
��D������m��2��2��0����
�ڡ�B��1��m2��4m+5����D������m��2��2��0����
��ֱ��DB�Ľ���ʽΪy=x+��m��2��2��
��B'������m��2��2��1����m��2��2+1 ����
��ֱ��PQ�Ľ���ʽΪy=x+2��m��2��2+2��
�߶���P�� ![]() ��2��m��2��2+
��2��m��2��2+ ![]() ����
����
��P����ֱ��PQ�ϣ�
��2��m��2��2+ ![]() ��=
��= ![]() +2��m��2��2+2��
+2��m��2��2+2��
��n=����m��2��2��
��n2+2n��8=0
��n=����m��2��2��
��n2+2n��8=0��
���n1=2��n2=��4��
�ੁ��m��2��2=2����ȥ����m��2��2=4��
��m1=4��m2=0
����������1����B��������֪��B���߶�OA�Ĵ�ֱƽ�����ϣ���֪OB=AB���ɵó��𰸣���2����m�ɱ�ʾ����ABO����������ö��κ��������ʿ������ȡ����Сֵʱ��m��ֵ����3���ٰ�B��������������߽���ʽ����m��ʾ��n��ֵ��������C��D�����ꣻ����B��D����ɱ�ʾ��ֱ��BD����ʽ����ƽ�ƿɱ�ʾ��B������꣬�Ӷ�����m��ʾ��ֱ��PQ�Ľ���ʽ������m��ʾ��P�����꣬����ֱ��PQ����ʽ����ɵõ�����m�ķ��̣������m��ֵ��
�����㾫����������Ҫ�����˶��κ�������ֵ�����֪ʶ�㣬��Ҫ��������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a������ȷ�����⣮

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�