题目内容
【题目】如图,在菱形ABCD中,∠BAD=120°,将菱形沿EF折叠,点B正好落在AD边的点G处,且EG⊥AC,若CD=8,则FG的长为( ) 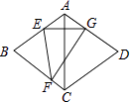
A.4 ![]()
B.4 ![]()
C.4 ![]()
D.6
【答案】B
【解析】解:如图,设AC与EG交于点O,FG交AC于H. 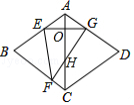
∵四边形ABCD是菱形,∠BAD=120°,
易证△ABC、△ACD是等边三角形,
∴∠CAD=∠B=60°,
∵EG⊥AC,
∴∠GOH=90°,
∵∠EGF=∠B=60°,
∴∠OHG=30°,
∴∠AGH=90°,
∴FG⊥AD,
∴FG是菱形的高,即等边三角形△ABC的高= ![]() ×8=4
×8=4 ![]() .
.
所以答案是B.
【考点精析】利用菱形的性质和翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目